
ЭЈЙ§дФЖСЫљЕУЕФЦєЪОЃЌЛиД№ЮЪЬт(дФЖСжаЕФНсТлПЩвджБНгЪЙгУ)ЃЎ
дФЖСЃКдкжБЯпЩЯгаnИіВЛЭЌЕФЕуЃЌдђДЫЭМжаЙВгаЖрЩйЬѕЯпЖЮЃП
ЭЈЙ§ЛЭМГЂЪдЃЌЮвУЧЗЂЯжСЫШчЯТЕФЙцТЩЃК
ЮЪЬтЃК(1)ФГбЇаЃЦпФъМЖЙВга8ИіАрМЖНјааБчТлБШШќЃЌЙцЖЈВЩгУЕЅбЛЗШќжЦ(УПСНИіАржЎМфШќвЛГЁ)ЃЌЧыЮЪИУаЃЦпФъМЖЕФБчТлШќЙВашНјааЖрЩйГЁБчТлШќЃП
(2)ЭљЗЕЩЯКЃгыББОЉжЎМфЕФФГЬЫЛ№ГЕЃЌЙВга15ИіГЕеО(АќРЈЩЯКЃгыББОЉ)ЃЌдђЙВашвЊзМБИЖрЩйжжВЛЭЌЕФГЕЦБЃП

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКдФЖСРэНт
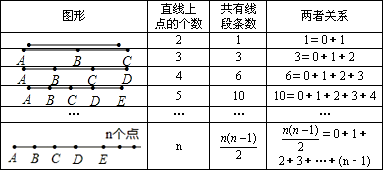
| ЭМаЮ | жБЯпЩЯЕуЕФИіЪ§ | ЙВгаЯпЖЮЬѕЪ§ | СНепЙиЯЕ | ||||
 |
2 | 1 | 1=0+1 | ||||
 |
3 | 3 | 3=0+1+2 | ||||
 |
4 | 6 | 6=0+1+2+3 | ||||
 |
5 | 10 | 10=0+1+2+3+4 | ||||
| Ё | Ё | Ё | Ё | ||||
 |
n |
|
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКжаЛЊЬтЭѕЁЁЪ§бЇЁЁЦпФъМЖЩЯЁЁ(ШЫНЬАц) ШЫНЬАц ЬтаЭЃК044
ЭЈЙ§дФЖСЫљЕУЕФЦєЪОЛиД№ЮЪЬтЃЎ(дФЖСжаЕФНсТлПЩжБНггУ)

ЮЪЬтЃКФГбЇаЃГѕШ§ЙВга8ИіАрНјааБчТлБШШќЃЌЙцЖЈНјааЕЅбЛЗШќ(УПСНИіАрШќвЛГЁ)ЃЌФЧУДЃЌИУГѕШ§ФъМЖЕФБчТлШќЙВНјааЖрЩйГЁДЮЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
| ЭМаЮ | жБЯпЩЯЕуЕФИіЪ§ | ЙВгаЯпЖЮЬѕЪ§ | СНепЙиЯЕ |
 | 2 | 1 | 1=0+1 |
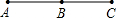 | 3 | 3 | 3=0+1+2 |
 | 4 | 6 | 6=0+1+2+3 |
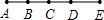 | 5 | 10 | 10=0+1+2+3+4 |
| Ё | Ё | Ё | Ё |
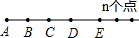 | n |  |  =0+1+2+3+Ё+ЃЈn-1ЃЉ =0+1+2+3+Ё+ЃЈn-1ЃЉ |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com