
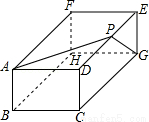
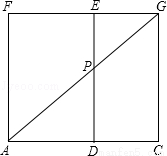
(2012•平谷区二模)如图是一个长方体,AB=3,BC=5,AF=6,要在长方体上系一根绳子连接AG,绳子与DE交于点P,当所用绳子的长最短时,AP的长为( )
A.10 B.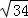 C.8 D.
C.8 D.
D
【解析】
试题分析:将长方体右侧的面展开,与上面的面在同一个平面内,如图所示,连接AG,此时所用的绳子最短,由正方体的中平行的棱长相等,得到DC=AB=EG=3,AD=BC=5,DE=AF=6,由EG与AD平行,得到两对内错角相等,利用两对对应角相等的两三角形相似可得出三角形EPG与三角形APD相似,由相似得比例,将EG,AD的长代入求出EP的长,进而求出PD的,在直角三角形APD中,由AD与PD的长,利用勾股定理即可求出AP的长.
【解析】
将长方体右侧的面展开,与上面的面在同一个平面内,连接AG,与ED交于P点,此时绳子的长最短,如图所示:
可得出:DC=AB=EG=3,AD=BC=5,DE=AF=6,
∵EG∥AD,
∴∠EGP=∠DAP,∠PEG=∠PDA,
∴△EPG∽△DPA,
∴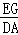 =
=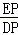 =
= ,即
,即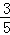 =
=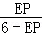 ,
,
解得:EP=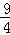 ,
,
∴PD=ED﹣EP=6﹣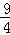 =
=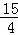 ,
,
在Rt△APD中,PD=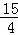 ,AD=5,
,AD=5,
根据勾股定理得:AP=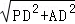 =
=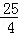 .
.
故选D


科目:初中数学 来源:2014-2015学年广东省东莞市八年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,在△ABC中,AB=AC,D、E在BC上,BD=CE,AF⊥BC于F,则图中全等三角形对数共有( )
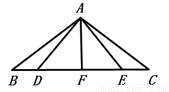
A.1对 B.2对 C.3对 D.4对
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 14.2勾股定理的应用练习卷(解析版) 题型:?????
(2013•余姚市模拟)已知:如图,无盖无底的正方体纸盒ABCD﹣EFGH,P,Q分别为棱FB,GC上的点,且FP=2PB,GQ=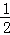 QC,若将这个正方体纸盒沿折线AP﹣PQ﹣QH裁剪并展开,得到的平面图形是( )
QC,若将这个正方体纸盒沿折线AP﹣PQ﹣QH裁剪并展开,得到的平面图形是( )
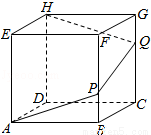
A.一个六边形
B.一个平行四边形
C.两个直角三角形
D.一个直角三角形和一个直角梯形
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 14.2勾股定理的应用练习卷(解析版) 题型:?????
(2014•平谷区一模)在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm.如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为( )
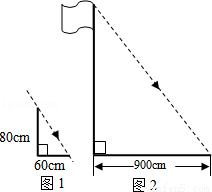
A.900cm B.1000cm C.1100cm D.1200cm
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.5逆命题与逆定理练习卷(解析版) 题型:?????
反证法证明“三角形中至少有一个角不小于60°”先应假设这个三角形中( )
A.有一个内角小于60° B.每个内角都小于60°
C.有一个内角大于60° D.每个内角都大于60°
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.1命题、定理与证明练习卷(解析版) 题型:?????
(2014•大庆)下列四个命题:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形;
(4)一组对边平行且相等的四边形是平行四边形.
其中正确的命题个数有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com