
 解:如图:∵正方形的四个顶点中有两个点的坐标为(0,0)、(2,2),
解:如图:∵正方形的四个顶点中有两个点的坐标为(0,0)、(2,2),

科目:初中数学 来源: 题型:
| AB |
| BA |
| AC |
| CA |
| AD |
| DA |
| BD |
| DB |
| AB |
| DC |
查看答案和解析>>
科目:初中数学 来源: 题型:
定义:在平面内,我们把既有大小又有方向的量叫做平面向量。平面向量可以用有向线段表示,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向。其中大小相等,方向相同的向量叫做相等向量。
如以正方形![]() 的四个顶点中某一点为起点,另一个顶点为终点作向量,可以作出8个不同
的四个顶点中某一点为起点,另一个顶点为终点作向量,可以作出8个不同
的向量:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() (由于
(由于![]() 和
和![]() 是相等向量,因此只算一个)。
是相等向量,因此只算一个)。
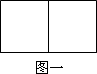
⑴ 作两个相邻的正方形(如图)。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
 |
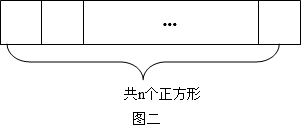
⑵ 作![]() 个相邻的正方形(如图)“
个相邻的正方形(如图)“![]() 一字型”排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为
一字型”排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
 …
…
共n个正方形
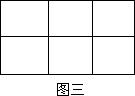
⑶ 作![]() 个相邻的正方形(如图)排开。以其中的一个顶点为起点,另一个顶点为终点作向量, 可以作出不同向量的个数记为
个相邻的正方形(如图)排开。以其中的一个顶点为起点,另一个顶点为终点作向量, 可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
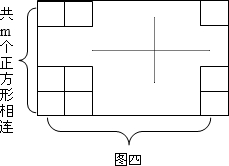
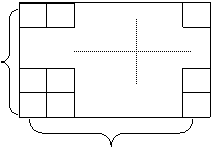
⑷ 作![]() 个相邻的正方形(如图四)排开。以其中的一个顶点为起点,另一个顶点为终点作向量, 可以作出不同向量的个数记为
个相邻的正方形(如图四)排开。以其中的一个顶点为起点,另一个顶点为终点作向量, 可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值。
的值。
| ||||
 | ||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com