
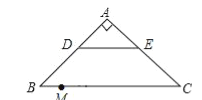
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 .
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】将点A(﹣3,4)绕原点顺时针方向旋转180°后得到点B,则点B的坐标为( )
A.(3,﹣4)B.(﹣4,3)C.(﹣4,﹣3)D.(﹣3,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
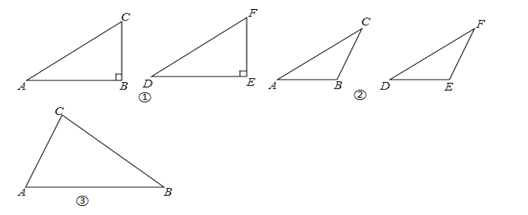
【题目】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据______,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若______,则△ABC≌△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
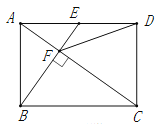
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
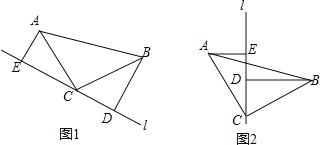
【题目】如图,△ABC中,∠ACB=90°,AC=BC,直线l过点C,BD⊥l,AE⊥l,垂足分别为D、E.
(1)当直线l不与底边AB相交时,求证:ED=AE+BD;
(2)如图2,将直线l绕点C顺时针旋转,使l与底边AB相交时,请你探究ED、AE、BD三者之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P1(x1,y1),点P2(x2,y2)是一次函数y=-3x-4图象上的两个点,且x1>x2,则y1与y2的大小关系是( )
A.y1=y2B.y1>y2C.y1<y2D.y1>y2>0
查看答案和解析>>
科目:初中数学 来源: 题型:
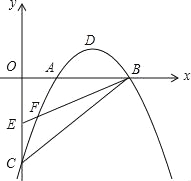
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.
(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com