
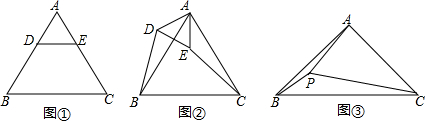
分析 (1)①由DE∥BC,得到 $\frac{DB}{AB}$=$\frac{EC}{AC}$,结合AB=AC,得到DB=EC;②由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;
(2)由旋转构造出△CPB≌△CEA,再用勾股定理计算出PE,然后用勾股定理逆定理判断出△PEA是直角三角形,在简单计算即可.
解答 解:(1)①∵DE∥BC,
∴$\frac{DB}{AB}$=$\frac{EC}{AC}$,
∵AB=AC,
∴DB=EC,
故答案为:=,
②成立.
证明:由①易知AD=AE,
∴由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中
$\left\{\begin{array}{l}{AD=AE}\\{∠DAB=∠EAC}\\{AB=AC}\end{array}\right.$,
∴△DAB≌△EAC,
∴DB=CE,
(2)如图,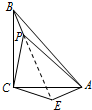
将△CPB绕点C旋转90°得△CEA,连接PE,
∴△CPB≌△CEA,
∴CE=CP=2,AE=BP=1,∠PCE=90°,
∴∠CEP=∠CPE=45°,
在Rt△PCE中,由勾股定理可得,PE=2 $\sqrt{2}$,
在△PEA中,PE2=(2 $\sqrt{2}$)2=8,AE2=12=1,PA2=32=9,
∵PE2+AE2=AP2,
∴△PEA是直角三角形
∴∠PEA=90°,
∴∠CEA=135°,
又∵△CPB≌△CEA
∴∠BPC=∠CEA=135°.
故答案为135°.
点评 此题是几何变换综合题,主要考查了旋转的性质,平行线的性质,全等三角形的性质和判定,勾股定理及其逆定理,解本题的关键是构造全等三角形,也是本题的难点.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:填空题
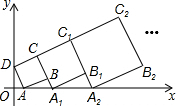 在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为5×($\frac{3}{2}$)4032.
在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为5×($\frac{3}{2}$)4032.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
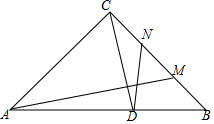 已知△ABC中,AC=BC,∠CAB=∠CBA=45°,点M为直线BC上任意一点,过点C作CD⊥AM交AB于点D,在BC上取一点N使CN=BM,连接DN
已知△ABC中,AC=BC,∠CAB=∠CBA=45°,点M为直线BC上任意一点,过点C作CD⊥AM交AB于点D,在BC上取一点N使CN=BM,连接DN查看答案和解析>>
科目:初中数学 来源: 题型:解答题
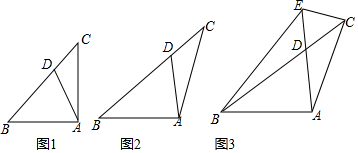
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
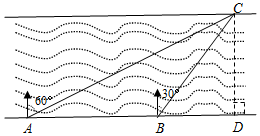 如图,在与南渡江对岸平行的岸边有A、B、D三点,A、B、D三点在同一直线上,在A点处测得河对岸C点在北偏东60°方向;从A点沿河边前进200米到达B点,这时测得C点在北偏东30°方向,
如图,在与南渡江对岸平行的岸边有A、B、D三点,A、B、D三点在同一直线上,在A点处测得河对岸C点在北偏东60°方向;从A点沿河边前进200米到达B点,这时测得C点在北偏东30°方向,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
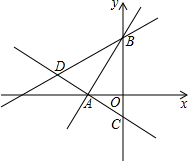 如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根.
如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com