
分析 作辅助线,构建直角三角形,设EH=a,EG=b,证明△AHE∽△BGE,列比例式得①式,在Rt△AEH中,根据勾股定理列②式,两式组成方程组解出可求得点E的坐标,与点A的坐标可求得旋转后的直线的解析式.
解答 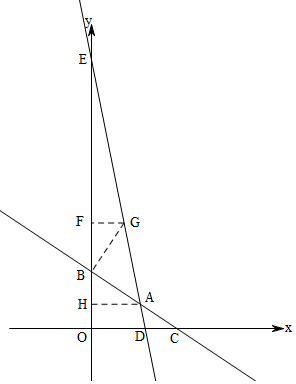 解:设旋转后的直线交y轴于E,交x轴于D,
解:设旋转后的直线交y轴于E,交x轴于D,
过A作AH⊥y轴于H,过B作BG⊥AB,交直线DE于G,
过G作GF⊥y轴于F,
由题意得:∠BAE=45°,A(2,1),
∴AH=2,OH=1,
直线AB的解析式为:y=-$\frac{2}{3}$x+$\frac{7}{3}$,
当x=0时,y=$\frac{7}{3}$,
∴BH=OB-OH=$\frac{7}{3}$-1=$\frac{4}{3}$,
∵∠BAG=45°,∠ABG=90°,
∴△ABG是等腰直角三角形,
∴AB=BG,
∵∠AHB=∠BFG=90°,∠ABH=∠BGF,
∴△AHB≌△BFG,
∴GF=BH=$\frac{4}{3}$,BF=AH=2,
∴G($\frac{4}{3}$,$\frac{13}{3}$),
设直线AG的解析式为:y=kx+b,
把G($\frac{4}{3}$,$\frac{13}{3}$),A(2,1)代入得:$\left\{\begin{array}{l}{\frac{4}{3}k+b=\frac{13}{3}}\\{2k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-5}\\{b=11}\end{array}\right.$,
∴直线AE的解析式为:y=-5x+11,
即所求的直线表达式为:y=-5x+11.
点评 本题考查了一次函数的旋转问题,有一定的难度,本题考查了利用待定系数法求一次函数的解析式、相似三角形的判定,勾股定理等知识,巧妙地利用相似和勾股定理列等式组成方程组解决此题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
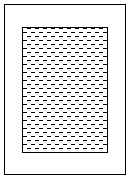 如图,用一张高为30cm,宽为20cm的长方形打印纸打印文档,如果左、右的页边距都为xcm,上、下页边距比左、右页边距多1cm.
如图,用一张高为30cm,宽为20cm的长方形打印纸打印文档,如果左、右的页边距都为xcm,上、下页边距比左、右页边距多1cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
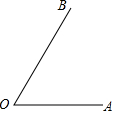 如图,∠AOB.(1)用尺规作出∠AOB的平分线OD;
如图,∠AOB.(1)用尺规作出∠AOB的平分线OD;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com