
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上)
(1)把△ABC绕点O按顺时针方向旋转90°,在网格中画出旋转后的△A1B1C1;
(2)如果网格中小正方形的边长为1,求点B旋转到B1所经过的弧形路径长.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源:2017届吉林长春德惠市九年级上期末数学试卷(解析版) 题型:解答题
如图,在∠ABC中,∠B=30°,AC= ,等腰直角△ACD斜边AD在AB边上,求BC的长.
,等腰直角△ACD斜边AD在AB边上,求BC的长.

查看答案和解析>>
科目:初中数学 来源:2017届湖北鄂州鄂城区九年级上期末数学试卷(解析版) 题型:解答题
已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源:2017届湖北鄂州鄂城区九年级上期末数学试卷(解析版) 题型:单选题
函数y= 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A.  B.
B. 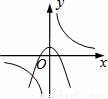 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017届黑龙江哈尔滨香坊区九年级上期末数学试卷(解析版) 题型:解答题
如图,四边形ACBE内接于⊙O,AB平分∠CAE,CD⊥AB交AB、AE分别于点H、D.

(1)如图①,求证:BD=BE;
(2)如图②,若F是弧AC的中点,连接BF,交CD于点M,∠CMF=2∠CBF,连接FO、OC,求∠FOC的度数;
(3)在(2)的条件下,连接OD,若BC=4 ,OD=7,求BF的长.
,OD=7,求BF的长.
查看答案和解析>>
科目:初中数学 来源:2017届黑龙江哈尔滨香坊区九年级上期末数学试卷(解析版) 题型:填空题
一个不透明的袋中只装有1个红球和2个蓝球,它们除颜色外其余均相同.现随机从袋中摸出两个球,颜色是一红一蓝的概率是 .
查看答案和解析>>
科目:初中数学 来源:2017届黑龙江哈尔滨香坊区九年级上期末数学试卷(解析版) 题型:选择题
下列说法中正确的是( )
A.平分弦的直径垂直于弦
B.圆心角是圆周角的2倍
C.三角形的外心到三角形各边的距离相等
D.从圆外一点可以引圆的两条切线,这一点和圆心的连线平分两条切线的夹角
查看答案和解析>>
科目:初中数学 来源:2017届河南省郑州市中考一模数学试卷(解析版) 题型:填空题
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC边上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为_____.

查看答案和解析>>
科目:初中数学 来源:2017届山东青岛李沧区九年级上期末数学试卷(解析版) 题型:解答题
(1)发现:
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:
如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段 AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com