
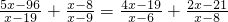 ;
;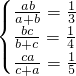 .
.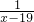 )+(1+
)+(1+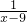 )=(4+
)=(4+ )+(2+
)+(2+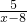 ),
),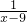 -
-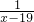 =
= +
+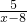 ,
,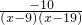 =
=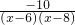 ,
,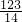 ,
,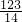 是原方程的解,
是原方程的解,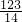 ;
;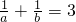 ①,
①,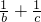 =4②,
=4②, =5③,
=5③,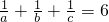 ④,
④, ,
, ,
, ,b=1,c=
,b=1,c= 是原方程的解,
是原方程的解,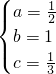 .
.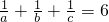 ④.
④.

 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
| 5x-96 |
| x-19 |
| x-8 |
| x-9 |
| 4x-19 |
| x-6 |
| 2x-21 |
| x-8 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| x |
| x-1 |
| x |
| x-1 |
| x2 |
| (x-1)2 |
| 4x |
| x-1 |
| x |
| x-1 |
| x |
| x-1 |
| x |
| x-1 |
| x |
| x-1 |
| 2x |
| x-1 |
| 4x |
| x-1 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
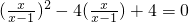 .
.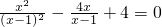 ,再去分母,行得通吗?
,再去分母,行得通吗? 是整体出现的!
是整体出现的! 看成一个整体,用y表示,即可设
看成一个整体,用y表示,即可设 =y,那么原方程就变为y2-4y+4=0.
=y,那么原方程就变为y2-4y+4=0. =2
=2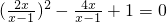
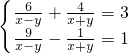 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 5x-96 |
| x-19 |
| x-8 |
| x-9 |
| 4x-19 |
| x-6 |
| 2x-21 |
| x-8 |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com