
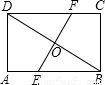
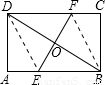
 解:如图,连接DE、BF,
解:如图,连接DE、BF, EF•BD=
EF•BD= ×30×40=600(米2).
×30×40=600(米2).

科目:初中数学 来源: 题型:
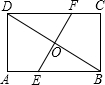 如图所示,有两条笔直的公路BD和EF(宽度不计),从一块矩形的土地ABCD中穿过,已知EF是BD的垂直平分线,BD=40米,EF=30 米,求四边形BEDF的面积.
如图所示,有两条笔直的公路BD和EF(宽度不计),从一块矩形的土地ABCD中穿过,已知EF是BD的垂直平分线,BD=40米,EF=30 米,求四边形BEDF的面积.查看答案和解析>>
科目:初中数学 来源:新课标 读想练同步测试 七年级数学(下) 北师大版 题型:068
如图所示,有一块正方形的土地,要在其上修建两条笔直的道路,将这片土地分成形状相同面积相等的四部分.若道路的宽度忽略不计,请设计三种不同的修筑方案(在给出的三张正方形图纸上分别画图,并简述画图的步骤).

查看答案和解析>>
科目:初中数学 来源:解题升级 七年级数学 题型:044
如图所示,在一条笔直的公路L两侧,分别有M、N两个村庄,现在要在公路L上建一供电站C,使供电站C到M、N两村所用电线之和最短.问供电站C的位置应该如何确定?

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
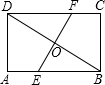 如图所示,有两条笔直的公路BD和EF(宽度不计),从一块矩形的土地ABCD中穿过,已知EF是BD的垂直平分线,BD=40米,EF=30 米,求四边形BEDF的面积.
如图所示,有两条笔直的公路BD和EF(宽度不计),从一块矩形的土地ABCD中穿过,已知EF是BD的垂直平分线,BD=40米,EF=30 米,求四边形BEDF的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com