

分析 (1)根据轴对称的性质可得∠EAF=∠DAE,AD=AF,再求出∠BAC=∠DAF,然后根据两边对应成比例,夹角相等两三角形相似证明;
(2)根据轴对称的性质可得EF=DE,AF=AD,再求出∠BAD=∠CAF,然后利用“边角边”证明△ABD和△ACF全等,根据全等三角形对应边相等可得CF=BD,全等三角形对应角相等可得∠ACF=∠B,然后求出∠ECF=90°,最后利用勾股定理证明即可;
(3)作点D关于AE的对称点F,连接EF、CF,根据轴对称的性质可得EF=DE,AF=AD,再根据同角的余角相等求出∠BAD=∠CAF,然后利用“边角边”证明△ABD和△ACF全等,根据全等三角形对应边相等可得CF=BD,全等三角形对应角相等可得∠ACF=∠B,然后求出∠ECF=90°,最后利用勾股定理证明即可.
解答 证明:(1)∵点D关于直线AE的对称点为F,
∴∠EAF=∠DAE,AD=AF,
又∵∠BAC=2∠DAE,
∴∠BAC=∠DAF,
∵AB=AC,
∴$\frac{AB}{AD}$=$\frac{AC}{AF}$,
∴△ADF∽△ABC;
(2)∵点D关于直线AE的对称点为F,
∴EF=DE,AF=AD,
∵α=45°,
∴∠BAD=90°-∠CAD,
∠CAF=∠DAE+∠EAF-∠CAD=45°+45°-∠CAD=90°-∠CAD,
∴∠BAD=∠CAF,
在△ABD和△ACF中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△ABD≌△ACF(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=2α,α=45°,
∴△ABC是等腰直角三角形,
∴∠B=∠ACB=45°,
∴∠ECF=∠ACB+∠ACF=45°+45°=90°,
在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,
所以,DE2=BD2+CE2;
(3)DE2=BD2+CE2还能成立.
理由如下:作点D关于AE的对称点F,连接EF、CF,
由轴对称的性质得,EF=DE,AF=AD,
∵α=45°,
∴∠BAD=90°-∠CAD,
∠CAF=∠DAE+∠EAF-∠CAD=45°+45°-∠CAD=90°-∠CAD,
∴∠BAD=∠CAF,
在△ABD和△ACF中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△ABD≌△ACF(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=2α,α=45°,
∴△ABC是等腰直角三角形,
∴∠B=∠ACB=45°,
∴∠BCF=∠ACB+∠ACF=45°+45°=90°,
∴∠ECF=180°-∠BCF=180°-90°=90°,
在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,
所以,DE2=BD2+CE2.
点评 本题是全等三角形的判定和性质、主要利用了轴对称的性质,同角的余角相等的性质,勾股定理,此类题目,小题间的思路相同是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
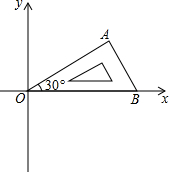 将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )| A. | ($\sqrt{3}$,-1) | B. | (1,-$\sqrt{3}$) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某班数学兴趣小组利用数学活动课时间测量位于烈山山顶的炎帝雕像高度,已知烈山坡面与水平面的夹角为30°,山高857.5尺,组员从山脚D处沿山坡向着雕像方向前进1620尺到达E点,在点E处测得雕像顶端A的仰角为60°,求雕像AB的高度.
某班数学兴趣小组利用数学活动课时间测量位于烈山山顶的炎帝雕像高度,已知烈山坡面与水平面的夹角为30°,山高857.5尺,组员从山脚D处沿山坡向着雕像方向前进1620尺到达E点,在点E处测得雕像顶端A的仰角为60°,求雕像AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,-2) | C. | (-1,2) | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com