
【题目】设抛物线的解析式为y=ax2 , 过点B1(1,0)作x轴的垂线,交抛物线于点A1(1,2);过点B2( ![]() ,0)作x轴的垂线,交抛物线于点A2;…;过点Bn((
,0)作x轴的垂线,交抛物线于点A2;…;过点Bn(( ![]() )n﹣1 , 0)(n为正整数)作x轴的垂线,交抛物线于点An , 连接AnBn+1 , 得Rt△AnBnBn+1 .
)n﹣1 , 0)(n为正整数)作x轴的垂线,交抛物线于点An , 连接AnBn+1 , 得Rt△AnBnBn+1 .
(1)求a的值;
(2)直接写出线段AnBn , BnBn+1的长(用含n的式子表示);
(3)在系列Rt△AnBnBn+1中,探究下列问题:
①当n为何值时,Rt△AnBnBn+1是等腰直角三角形?
②设1≤k<m≤n(k,m均为正整数),问:是否存在Rt△AkBkBk+1与Rt△AmBmBm+1相似?若存在,求出其相似比;若不存在,说明理由.
【答案】
(1)
解:如图1所示,
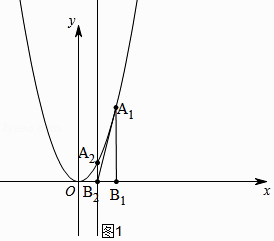
∵点A1(1,2)在抛物线的解析式为y=ax2上,
∴a=2
(2)
解:如图2所示,
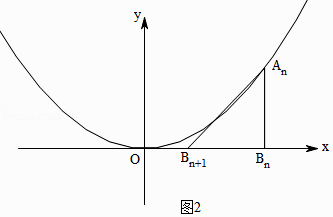
AnBn=2x2=2×[( ![]() )n﹣1]2=
)n﹣1]2= ![]() ,BnBn+1=
,BnBn+1= ![]()
(3)
解:如图3所示,
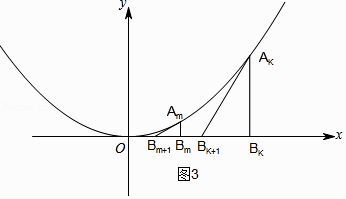
由Rt△AnBnBn+1是等腰直角三角形得AnBn=BnBn+1,则: ![]() =
= ![]() ,
,
2n﹣3=n,n=3,
∴当n=3时,Rt△AnBnBn+1是等腰直角三角形,
②依题意得,∠AkBkBk+1=∠AmBmBm+1=90°,
有两种情况:i)当Rt△AkBkBk+1∽Rt△AmBmBm+1时,
![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
所以,k=m(舍去),
ii)当Rt△AkBkBk+1∽Rt△Bm+1BmAm时,
![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴k+m=6,
∵1≤k<m≤n(k,m均为正整数),
∴取 ![]() 或
或 ![]() ;
;
当 ![]() 时,Rt△A1B1B2∽Rt△B6B5A5,
时,Rt△A1B1B2∽Rt△B6B5A5,
相似比为: ![]() =
= ![]() =64,
=64,
当 ![]() 时,Rt△A2B2B3∽Rt△B5B4A4,
时,Rt△A2B2B3∽Rt△B5B4A4,
相似比为: ![]() =
= ![]() =8,
=8,
所以:存在Rt△AkBkBk+1与Rt△AmBmBm+1相似,其相似比为64:1或8:1.
【解析】(1)直接把点A1的坐标代入y=ax2求出a的值;(2)由题意可知:A1B1是点A1的纵坐标:则A1B1=2×12=2;A2B2是点A2的纵坐标:则A2B2=2×( ![]() )2=
)2= ![]() ;…则AnBn=2x2=2×[(
;…则AnBn=2x2=2×[( ![]() )n﹣1]2=
)n﹣1]2= ![]() ;
;
B1B2=1﹣ ![]() =
= ![]() ,B2B3=
,B2B3= ![]() ﹣
﹣ ![]() =
= ![]() =
= ![]() ,…,BnBn+1=
,…,BnBn+1= ![]() ;(3)因为Rt△AkBkBk+1与Rt△AmBmBm+1是直角三角形,所以分两种情况讨论:根据(2)的结论代入所得的对应边的比列式,计算求出k与m的关系,并与1≤k<m≤n(k,m均为正整数)相结合,得出两种符合条件的值,分别代入两相似直角三角形计算相似比.
;(3)因为Rt△AkBkBk+1与Rt△AmBmBm+1是直角三角形,所以分两种情况讨论:根据(2)的结论代入所得的对应边的比列式,计算求出k与m的关系,并与1≤k<m≤n(k,m均为正整数)相结合,得出两种符合条件的值,分别代入两相似直角三角形计算相似比.


科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.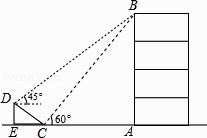
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在 ![]() 上且不与A点重合,但Q点可与B点重合.
上且不与A点重合,但Q点可与B点重合. 
发现: ![]() 的长与
的长与 ![]() 的长之和为定值l,求l:
的长之和为定值l,求l:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
B.审查书稿中有哪些学科性错误适合用抽样调查法
C.甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
D.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象分别交于
的图象分别交于![]() ,
,![]() 两点,已知点
两点,已知点![]() 与点
与点![]() 关于坐标原点
关于坐标原点![]() 成中心对称,且点
成中心对称,且点![]() 的坐标为
的坐标为![]() .其中
.其中![]() .
.
(1)四边形![]() 是 .(填写四边形
是 .(填写四边形![]() 的形状)
的形状)
(2)当点![]() 的坐标为
的坐标为![]() 时,且四边形
时,且四边形![]() 是矩形,求
是矩形,求![]() ,
,![]() 的值.
的值.
(3)试探究:随着![]() 与
与![]() 的变化,四边形
的变化,四边形![]() 能不能成为菱形?若能,请直接写出
能不能成为菱形?若能,请直接写出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B表示的数分别为-3,0,1,点P为数轴上任意一点,其表示的数为x.
(1)如果点P到点A,点B的距离相等,那么x=______;
(2)若点P到点A,点B的距离之和最小,则整数x是____________ ;
(3)当点P到点A,点B的距离之和是6时,求x的值;
(4)若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动多少秒时,点P到点E,点F的距离相等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com