
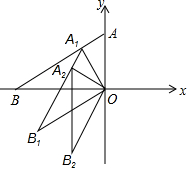
 如图,点A(0,1),点B(-$\sqrt{3}$,0),作OA1⊥AB,垂足为A1,以OA1为边作Rt△A1OB1,使∠A1OB1=90°,∠B1=30°,作OA2⊥A1B1,垂足为A2,再以OA2为边作Rt△A2OB2,使∠A2OB2=90°,∠B2=30°,…,以同样的作法可得到Rt△AnOBn,则当n=2017时,点A2017的纵坐标为( )
如图,点A(0,1),点B(-$\sqrt{3}$,0),作OA1⊥AB,垂足为A1,以OA1为边作Rt△A1OB1,使∠A1OB1=90°,∠B1=30°,作OA2⊥A1B1,垂足为A2,再以OA2为边作Rt△A2OB2,使∠A2OB2=90°,∠B2=30°,…,以同样的作法可得到Rt△AnOBn,则当n=2017时,点A2017的纵坐标为( )| A. | ($\frac{\sqrt{3}}{2}$)2017 | B. | -($\frac{\sqrt{3}}{2}$)2017 | C. | ($\frac{\sqrt{3}}{2}$)2018 | D. | -($\frac{\sqrt{3}}{2}$)2018 |
分析 由每次旋转30°可知,点所在的射线以12为周期循环,所以A2017在射线OA1上,故排除B、D,再找到三角形的变化规律即可解题.
解答 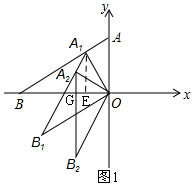 解:在Rt△AOB中,OA=1,OB=$\sqrt{3}$,
解:在Rt△AOB中,OA=1,OB=$\sqrt{3}$,
∴∠ABO=30°,
∵OA1⊥AB,
∴A1O=$\frac{1}{2}$OB=$\frac{\sqrt{3}}{2}$,∠AOA1=30°,
可知每次逆时针旋转30°,点所在的射线以12为周期循环,
∵且每次旋转后,原三角形的高变新的直角边,
∴三角形依次减小,且相似比为$\frac{\sqrt{3}}{2}$,
2017÷12=168…余1,所以当n=2017时,点A2017的纵坐标与A1的纵坐标在同一条射线上,
且OA2017=${(\frac{\sqrt{3}}{2})}^{2017}$,
过点A1作A1E⊥OB于E,
∴∠EA1O=30°,
∴OE=$\frac{1}{2}$A1O=$\frac{\sqrt{3}}{4}$,A1的纵坐标=A1E=($\frac{\sqrt{3}}{2}$)2=$\frac{\sqrt{3}}{2}$OA1,
点A2017的纵坐标为$\frac{\sqrt{3}}{2}$OA2017=${(\frac{\sqrt{3}}{2})}^{2018}$,
故选C.
点评 本题考查了含30°直角三角形的性质,考查了相似三角形规律的发现,本题中根据相似比求OA2017的长是解题的关键.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源:2017届辽宁省九年级3月月考数学试卷(解析版) 题型:单选题
小明从二次函数y=ax2+bx+c的图象(如图)中观察得出了下面五条信息:①c<0;②abc>0;③a﹣b+c>0;④2a﹣3b=0;⑤c﹣4b>0.你认为其中正确的信息是( )
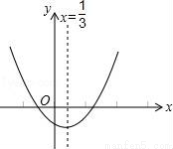
A. ①②③⑤ B. ①②③④ C. ①③④⑤ D. ②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
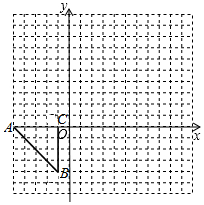 如图,直角坐标系中的△ABC的三个顶点分别为A(-5,0),B(-1,-4),C(-1,0).
如图,直角坐标系中的△ABC的三个顶点分别为A(-5,0),B(-1,-4),C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 抛物线y=x2-2mx+m2-4与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,抛物线的对称轴为x=1.
抛物线y=x2-2mx+m2-4与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,抛物线的对称轴为x=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
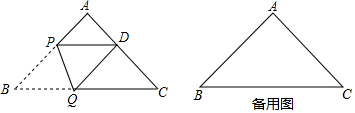
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
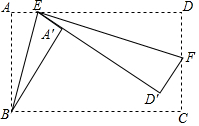 如图,矩形ABCD中,AB=8,BC=15,点E是AD边上一点,连接BE,把△ABE沿BE折叠,使点A落在点A′处,点F是CD边上一点,连接EF,把△DEF沿EF折叠,使点D落在直线EA′上的点D′处,当点D′落在BC边上时,AE的长为$\frac{15+\sqrt{33}}{3}$或$\frac{15-\sqrt{33}}{3}$.
如图,矩形ABCD中,AB=8,BC=15,点E是AD边上一点,连接BE,把△ABE沿BE折叠,使点A落在点A′处,点F是CD边上一点,连接EF,把△DEF沿EF折叠,使点D落在直线EA′上的点D′处,当点D′落在BC边上时,AE的长为$\frac{15+\sqrt{33}}{3}$或$\frac{15-\sqrt{33}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com