
如图所示中分别给出了锐角三角形、直角三角形、钝角三角形.
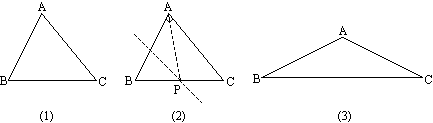
(1)请动手作出到三个顶点A、B、C距离相等的点P,并指出P与△ABC的位置关系;
(2)求证:如图所示(2)中的点P是斜边BC的中点.
|
解: (1)学生画图:点P分别在锐角△ABC内部;在Rt△ABC的边BC上;在钝角△ABC的外部.(2)证明:如图(2),作AB的垂直平分线交斜边BC于P,连接PA,则有PB=PA(线段垂直平分线上的点到线段两端的距离相等). ∴∠ B=∠PAB(等边对等角).又∵∠ B+∠C=∠ PAB+∠PAC=∴∠ PAC=∠C(等量代换)∴ PA=PC(等角对等边)∴ P在AC的垂直平分线上(垂直平分线的判定)∴ P是三边垂直平分线的交点.且 PA=PB=PC,∴P是斜边BC的中点. |
|
思维 (1)作三边垂直平分线,其交点就是求作的点P.(2)证P是BC的中点的思路是,作AB的垂直平分线交斜边于P;只要证明P在AC的垂直平分线上,则有PB=PA=PC,即P是BC中点. 特别提示:由于 PA=PB=PC,所以得出结论:直角三角形斜边上的中线等于斜边的一半. |


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
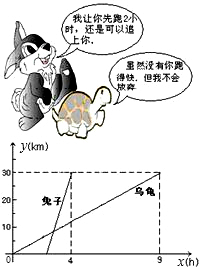 龟兔赛跑中,由于兔子途中睡大觉结果输给了乌龟,事后兔子认真总结教训又约乌龟进行了一次比赛,二者从森林甲地出发到森林乙地,赛跑过程中路程随时间变化的图象如图所示
龟兔赛跑中,由于兔子途中睡大觉结果输给了乌龟,事后兔子认真总结教训又约乌龟进行了一次比赛,二者从森林甲地出发到森林乙地,赛跑过程中路程随时间变化的图象如图所示查看答案和解析>>
科目:初中数学 来源: 题型:
 21、小林在帮姥姥做清洁时不小心打碎了装饰柜门上的一块三角形玻璃(碎后形状如图所示),小林决定用自己积攒的零花钱到玻璃店给买一块一样大小的玻璃,请父亲给安装好.
21、小林在帮姥姥做清洁时不小心打碎了装饰柜门上的一块三角形玻璃(碎后形状如图所示),小林决定用自己积攒的零花钱到玻璃店给买一块一样大小的玻璃,请父亲给安装好.查看答案和解析>>
科目:初中数学 来源: 题型:
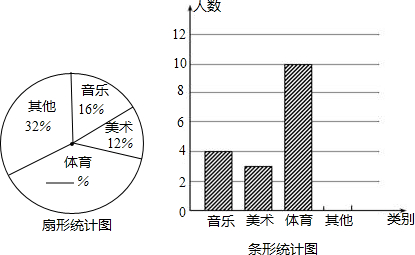
 (2013•黔西南州)“五一”假期,黔西南州某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图所示是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:
(2013•黔西南州)“五一”假期,黔西南州某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图所示是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com