Question

20．平面直角坐标中，函数y=kx-k（k＞0）的图象与函数y=$\frac{4}{x}$（x＞0）的图象交于点为A（m，2）与y轴交于点B，若点P是x轴上一点，且满足△PAB的面积是6，则P点的坐标为（4，0），（-2，0）．

Answer 1

分析 将A点坐标代入y=$\frac{4}{x}$（x＞0），求出m的值为2，再将（2，2）代入y=kx-k，求出k的值，并根据一次函数的解析式求得直线与坐标轴的交点B、C的坐标，最后将△ABP以x轴为分界线，分为两个三角形进行计算，求得CP的长，进而确定点P的位置．

解答 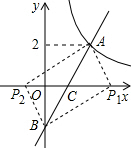解：将A（m，2）代入y=$\frac{4}{x}$（x＞0）得，m=2
∴A点坐标为A（2，2）
将A（2，2）代入y=kx-k得，2k-k=2
解得k=2
∴一次函数解析式为y=2x-2
∵一次函数y=2x-2与x轴的交点为C（1，0），与y轴的交点为B（0，-2）
∵S_△ABP=S_△ACP+S_△BPC
∴$\frac{1}{2}$×2×CP+$\frac{1}{2}$×2×CP=6
解得CP=3
∴当P在C的右侧时，OP=3+1=4；当P在C的左侧时，OP=3-1=2
∴P点坐标为（4，0），（-2，0）
故答案为：（4，0），（-2，0）

点评 本题主要考查了反比例函数与一次函数的交点问题，解决问题的关键是根据S_△ABP=S_△ACP+S_△BPC，确定CP的长．在解题时注意：△ABP中点P的位置可能在点C的左侧，也可能在点C的左侧，需要分类讨论．