
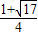 ,x2=
,x2=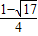 ,则有x1+x2=
,则有x1+x2= ,x1x2=-1.
,x1x2=-1. ,x2=1,则有x1+x2=-
,x2=1,则有x1+x2=- ,x1x2=-
,x1x2=- .
. ,
,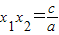 .
.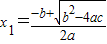 ,
,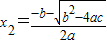 .
.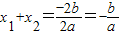 ,
,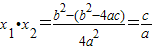 ,
,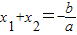 ,
,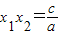 .
. ,
,

科目:初中数学 来源:2010年浙江省杭州市萧山区中考数学模拟试卷45(南阳初中 刘东旭 金凯)(解析版) 题型:解答题
 ≥0,∴a-
≥0,∴a- +b≥0,∴a+b≥2
+b≥0,∴a+b≥2 ,只有点a=b时,等号成立.
,只有点a=b时,等号成立. (a,b均为正实数)中,若ab为定值p,则a+b≥
(a,b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2 .
.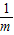 有最小值______;
有最小值______; ,并指出等号成立时的条件;
,并指出等号成立时的条件; 上的任意一点,过点P作PC⊥x轴于点C,PO⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
上的任意一点,过点P作PC⊥x轴于点C,PO⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《概率》(05)(解析版) 题型:解答题
| 种类 | 频数 | 频率 |
| 科普 | 0.15 | |
| 艺术 | 78 | |
| 文学 | 0.59 | |
| 其它 | 81 |
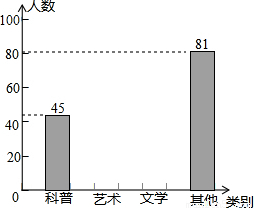
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《一元二次方程》(04)(解析版) 题型:解答题
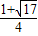 ,x2=
,x2=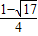 ,则有x1+x2=
,则有x1+x2= ,x1x2=-1.
,x1x2=-1. ,x2=1,则有x1+x2=-
,x2=1,则有x1+x2=- ,x1x2=-
,x1x2=- .
.查看答案和解析>>
科目:初中数学 来源:2009年北京市延庆县中考数学一模试卷(解析版) 题型:解答题
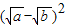 ≥0,∴a-
≥0,∴a-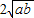 +b≥0,∴a+b≥2
+b≥0,∴a+b≥2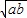 ,只有点a=b时,等号成立.
,只有点a=b时,等号成立.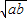 (a,b均为正实数)中,若ab为定值p,则a+b≥
(a,b均为正实数)中,若ab为定值p,则a+b≥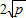 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2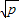 .
.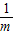 有最小值______;
有最小值______;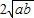 ,并指出等号成立时的条件;
,并指出等号成立时的条件;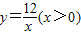 上的任意一点,过点P作PC⊥x轴于点C,PO⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
上的任意一点,过点P作PC⊥x轴于点C,PO⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.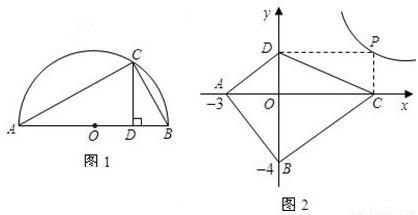
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com