练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．化简：（1-$\frac{3}{x+1}$）÷$\frac{{x}^{2}-4}{x+1}$．

    分析 根据分式的减法和除法可以解答本题．

    解答 解：（1-$\frac{3}{x+1}$）÷$\frac{{x}^{2}-4}{x+1}$
    =$\frac{x+1-3}{x+1}•\frac{x+1}{（x+2）（x-2）}$
    =$\frac{x-2}{x+1}•\frac{x+1}{（x+2）（x-2）}$
    =$\frac{1}{x+2}$．

    点评 本题考查分式的混合运算，解答本题的关键是明确分式的混合运算的计算方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    18．分式方程$\frac{4}{a-3}$=$\frac{1}{a}$的根是a=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

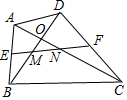    13．如图．在四边形ABCD中．AC=BD，E，F分别为AB，CD的中点（O，M，N不重合），仔细观察你会发观．无论四边形ABCD的形状如何变化，只要保待对角线相等，则EF与两条对角线围成的三角形总是等腰三角形（图中的△OMN），请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．现有一根长为1米的木杆，第1次截取其长度的一半，第2次截取其第1次剩下长度的一半，第3次截取其第2次剩下长度的一半，如此反复截取，则第n（n为正整数）次截取后，此木杆剩下的长度为$\frac{1}{{2}^{n}}$米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图1，二次函数y=ax2+bx-4（a≠0）的图象与x轴交于A（3，0），B（-1，0）两点，与y轴交于点C．
    （1）求该二次函数的解析式及点C的坐标；
    （2）设该抛物线的顶点为D，求△ACD的面积；
    （3）若点P，Q同时从A点出发，如图2（注：图2与图1完全相同），都以每秒1个单位长度的速度分别沿线段AB，AC运动，当其中一点到达终点时，另一点也随之停止运动，当P，Q运动到t秒时，将△APQ沿PQ所在直线翻折，点A恰好落在抛物线上E处，判定此时四边形APEQ的形状，说明理由，并求出点E的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

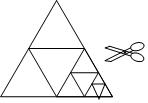    7．在一次数学综合实践课上，某同学将一张等边三角形纸片沿中位线剪成4个小三角形．称为第一次操作；然后，将其中的一个三角形按同样方式再剪成4个小三角形，共得到7个小三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得到10个小三角形，称为第三次操作；…根据以上操作，若要得到100个小三角形，则需要操作的次数是（　　）
    A．25B．34C．33D．50

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．四边形ABCD的对角线交于点E，且AE=EC，BE=ED，以AB为直径的半圆过点E，圆心为O．
    （1）利用图1，求证：四边形ABCD是菱形．
    （2）如图2，若CD的延长线与半圆相切于点F，且直径AB=8．
    ①△ABD的面积为16．
    ②$\widehat{BE}$的长$\frac{2}{3}$π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．当2a-2b+5=0时，求$\frac{{a}^{2}-2ab}{a-b}$-$\frac{{b}^{2}}{b-a}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．若二次根式$\frac{\sqrt{m-2}}{|{m}^{2}-m-2|}$有意义，则m的取值范围是m＞2．

    查看答案和解析>>

    同步练习册答案