
 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
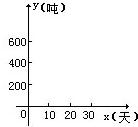 29、某工厂有甲、乙两条生产线先后投产.在乙生产线投产以前,甲生产线已生产了200吨成品;从乙生产线投产开始,甲、乙两条生产线每天分别生产20吨和30吨成品.
29、某工厂有甲、乙两条生产线先后投产.在乙生产线投产以前,甲生产线已生产了200吨成品;从乙生产线投产开始,甲、乙两条生产线每天分别生产20吨和30吨成品.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
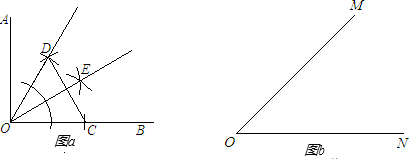
 的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: )、R(b,
)、R(b, ),求直线OM对应的函数关系式(用含a、b的代数式表示).
),求直线OM对应的函数关系式(用含a、b的代数式表示). ∠AOB.
∠AOB.
查看答案和解析>>
科目:初中数学 来源:2010年江苏省无锡市江南中学中考数学二模试卷(解析版) 题型:解答题
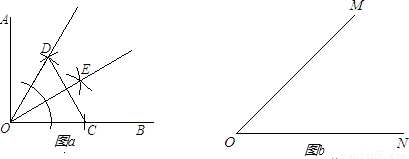
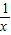 的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: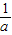 )、R(b,
)、R(b,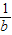 ),求直线OM对应的函数关系式(用含a、b的代数式表示).
),求直线OM对应的函数关系式(用含a、b的代数式表示). ∠AOB.
∠AOB.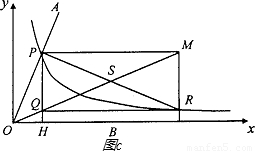
查看答案和解析>>
科目:初中数学 来源:2011年江苏省无锡市育才中学中考数学二模试卷(解析版) 题型:解答题

 的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: )、R(b,
)、R(b, ),求直线OM对应的函数关系式(用含a、b的代数式表示).
),求直线OM对应的函数关系式(用含a、b的代数式表示). ∠AOB.
∠AOB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com