
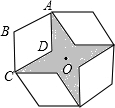
 如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=2,则图中阴影部分的面积为
如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=2,则图中阴影部分的面积为 解:如图所示:连接AC,BD交于点E,连接DF,FM,MN,DN,
解:如图所示:连接AC,BD交于点E,连接DF,FM,MN,DN,| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
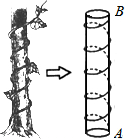 我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是
我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是查看答案和解析>>
科目:初中数学 来源: 题型:
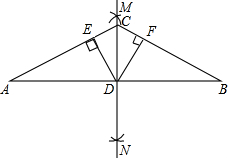 如图,分别以线段AB的两个端点为圆心,大于AB的长为半径作弧,两弧交于M、N两点,连接MN,交AB于点D、C是直线MN上任意一点,连接CA、CB,过点D作DE⊥AC于点E,DF⊥BC于点F.
如图,分别以线段AB的两个端点为圆心,大于AB的长为半径作弧,两弧交于M、N两点,连接MN,交AB于点D、C是直线MN上任意一点,连接CA、CB,过点D作DE⊥AC于点E,DF⊥BC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com