
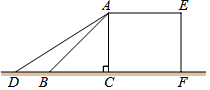
 如图,某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示. AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为45°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD 是改造后的斜坡(点D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)[参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.601,$\sqrt{2}$≈1.414].
如图,某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示. AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为45°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD 是改造后的斜坡(点D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)[参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.601,$\sqrt{2}$≈1.414]. 分析 首先根据∠ABC=45°,AB=2m,在Rt△ABC中,求出AC的长度,然后根据∠ADC=31°,利用三角函数的知识在Rt△ACD中求出CD的长度.
解答 解:在Rt△ABC中,
∵∠ABC=53°,AB=2m,
∴AC=AB•sin45°=2$\sqrt{2}$(m)
∴$AC=BC=\sqrt{2}m$,
在Rt△ADC中,∵∠ADC=31°,
∴$tan∠ADC=\frac{AC}{DC}$,
∴$DC=\frac{AC}{tan∠ADC}=\frac{{\sqrt{2}}}{{tan{{31}^0}}}≈2.36m$.
答:斜坡AD底端D与平台AC的距离CD约为2.36m.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据坡角构造之间三角形,利用三角函数的知识解直角三角形.


科目:初中数学 来源: 题型:选择题
| A. | 2×32=36 | B. | -32=-9 | C. | 3÷$\frac{3}{2}×\frac{2}{3}$=3 | D. | -5-|-2|=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三角形的角平分线是射线 | |
| B. | 过三角形一边中点的线段一定是三角形的中线 | |
| C. | 三条线段一定能组成一个三角形 | |
| D. | 三角形的中线是线段 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com