分析:从图中可以看出,正方形的边长=a+b,所以面积=(a+b)
2,矩形的长和宽分别是2a+b,b,面积=b(a+2b),两图形面积相等,列出方程得=(a+b)
2=b(a+2b),其中a=1,求b的值,即可求得正方形的面积.
解答:根据图形和题意可得:
(a+b)
2=b(a+2b),
其中a=1,
则方程是(1+b)
2=b(1+2b)
解得:b=

所以正方形的面积为(1+

)
2=
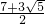
,
故答案为:
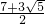
.
点评:此题主要考查了图形的剪拼,本题的关键是从两图形中,找到两图形的边长的值,然后利用面积相等列出等式求方程,解得b的值,从而求出边长,求面积.

