(1)在Rt△ABC中,∠C=90°,AB=17,AC=8,则BC=______.
(2)在Rt△ABC中,∠C=90°,AC=5,BC=12.则AB=______.
(3)在Rt△ABC中,∠C=90°,AC:AB=3:4,AB=25,则AC=______,BC=______.
(4)在Rt△ABC中,AB=6,AC=8,则BC=______.
解:(1)在Rt△ABC中,∠C=90°,AB=17,AC=8,则BC=

=15.
(2)在Rt△ABC中,∠C=90°,AC=5,BC=12.则AB=

=13.
(3)在Rt△ABC中,∠C=90°,AC:AB=3:4,AB=25,则AC=
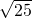
×3=15,BC=
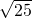
×4=20.
(4)①当AB、AC为直角边时,根据勾股定理得:
BC=

=10,
②当AC为斜边,AB为直角边时,根据勾股定理得:
BC=
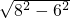
=2

.
故BC=10或2

.
故答案为:15;13;15,20;10或2

.
分析:(1)根据勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,即BC
2+AC
2=AB
2,结合AB=17,AC=8,可求出另一条直角边BC的长度;
(2)根据勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,即BC
2+AC
2=AB
2,结合AC=5,BC=12,可求出斜边AB的长度;
(3)根据勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方即可求解.
(4)从当此直角三角形的两直角边分别是6和8时,当此直角三角形的一个直角边为6,斜边为8时这两种情况分析,再利用勾股定理即可求出第三边.
点评:本题考查了勾股定理的知识,解答的关键是熟练掌握勾股定理的定义及其在直角三角形中的表示形式.

 =15.
=15. =13.
=13.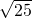 ×3=15,BC=
×3=15,BC=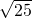 ×4=20.
×4=20. =10,
=10,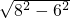 =2
=2 .
. .
. .
.
