练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    某同学的身高为1.4m，某一时刻他在阳光下的影长为1.2m．此时，与他相邻的一棵小树的影长为3.6m，这棵树的高度为
     
    m．
    考点：相似三角形的应用
    专题：
    分析：设这棵树高度为h，根据同一时刻物高与影长成正比列出关于h的方程，求出h的值即可．
    解答：解：解：设这棵树高度为hm，
    ∵同一时刻物高与影长成正比，
    ∴
    1.4
    1.2
    =
    h
    3.6
    ，
    解得h=4.2．
    故答案为：4.2．
    点评：本题考查了相似三角形的应用，熟知同一时刻物高与影长成正比是解答此题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

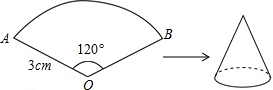    如图，已知扇形AOB的半径为3cm，圆心角的度数为120°，若将此扇形围成一个圆锥，则围成的圆锥的侧面积为（　　）
    A、πcm2
    B、2πcm2
    C、3πcm2
    D、6πcm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：（
    		15
    -
    		10
    ）÷
    		5
    ×（-
    		50
    ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：（
    1
    3
    a+3b）2-（
    1
    3
    a-3b）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在一次数学实践活动中，某学习小组用测倾器和皮尺测出了一座小山的高度，请你依据这两件测量工具按要求完成以下任务：
    （1）参考所给图形，画出测量小山高度MN的示意图；
    （2）写出一套测量山高的设计方案；
    （3）用字母表示测量数据，写出求得山高的计算式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若2x2-x+1=0，则3-4x2+2x=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    （1）3×（-4）+（-28）÷（-7）
    （2）
    11
    5
    ×（
    3
    1
    27
    -
    1
    2
    ）×
    3
    11
    ÷|-
    5
    4
    |    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：6tan230°-
    		3
    sin60°-2cos45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）计算：
    sin245°+tan60°•cos30°
    		2
    cos45°+tan45°
    -|
    		3
    -2|-
    1
    2-
    		3
    +
    38
    +（
    1
    		5
    -1
    ）0
    （2）解方程：（5x-1）（x+1）=2x+3．

    查看答案和解析>>

    同步练习册答案