
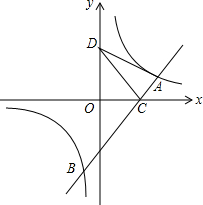
 如图所示,已知A(4,m),B(-1,n)在反比例函数y=$\frac{8}{x}$的图象上,直线AB与x轴交于C,如果点D在y轴上,且DA=DC.
如图所示,已知A(4,m),B(-1,n)在反比例函数y=$\frac{8}{x}$的图象上,直线AB与x轴交于C,如果点D在y轴上,且DA=DC.分析 (1)将A与B坐标代入反比例解析式求出m与n的值,确定出A与B坐标,设直线AB解析式为y=kx+b,将A与B坐标代入求出k与b的值,确定出直线AB解析式,即可求出C坐标;
(2)设点D坐标为(0,m),由DA=DC根据两点间距离公式列出方程,求出m的值即可.
解答 解:(1)将A(4,m),B(-1,n)代入y=$\frac{8}{x}$得:m=2,n=-8,
即A(4,2),B(-1,-8),
设直线AB解析式为y=kx+b,
将A与B坐标代入得:$\left\{\begin{array}{l}{4k+b=2}\\{-k+b=-8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-6}\end{array}\right.$,即直线AB解析式为y=2x-6,
令y=0,得到x=3,
即C(3,0);
(2)设点D坐标为(0,m),
∵DA=DC,
∴$\sqrt{{4}^{2}+(2-m)^{2}}$=$\sqrt{{3}^{2}+{m}^{2}}$,
解得:m=$\frac{11}{4}$,
则D(0,$\frac{11}{4}$).
点评 此题考查了一次函数与反比例函数的交点问题,利用了待定系数法及数形结合思想,熟练掌握待定系数法是解本题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
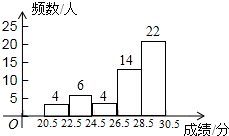 九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )
九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )| A. | 80% | B. | 70% | C. | 92% | D. | 86% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.
如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在0C上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达0C′的位置.已知0A=8cm,AB⊥0C,∠B0A=60°,sin∠B′A0=$\frac{9}{10}$,则点B′到0A的距离为( )
如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在0C上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达0C′的位置.已知0A=8cm,AB⊥0C,∠B0A=60°,sin∠B′A0=$\frac{9}{10}$,则点B′到0A的距离为( )| A. | $\frac{9\sqrt{3}}{10}$cm | B. | $\frac{18\sqrt{3}}{10}$cm | C. | $\frac{9\sqrt{3}}{5}$cm | D. | $\frac{18\sqrt{3}}{5}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com