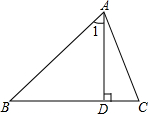
如图.AD是△ABC的高.∠1=∠B.∠C=65°.则∠BAC=70°．题目和参考答案——青夏教育精英家教网—

8．

如图，AD是△ABC的高，∠1=∠B，∠C=65°，则∠BAC=70°．

分析先根据AD是△ABC的高得出∠ADB=90°，再由∠1=∠B得出∠B的度数，由三角形内角和定理可得出结论．

解答解：∵AD是△ABC的高，
∴∠ADB=90°．
∵∠1=∠B，
∴∠B=45°．
∵∠C=65°，
∴∠BAC=180°-65°-45°=70°．
故答案为：70．

点评本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．

练习册系列答案

高中得分王系列答案

相关习题

科目：初中数学 来源： 题型：解答题

18．

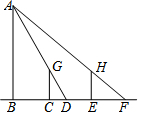如图，王华晚上由路灯下的B处走到C处时，测得影子CD的长为1米，继续往前走3米到达E处时，测得影子EF的长为2米，已知王华的身高是1.5米．求路灯A到直线CD的距离．

科目：初中数学 来源： 题型：选择题

19．若2a^xb³与-3a²b^y的和为单项式，则y^x是（　　）

A．

B．

C．

D．

科目：初中数学 来源： 题型：选择题

16．运用加法的运算律计算（+6$\frac{1}{3}$）+（-18）+（+4$\frac{2}{3}$）+（-6.8）+18+（-3.2）最适当的是（　　）

	A．	[（+6$\frac{1}{3}$）+（+4$\frac{2}{3}$）+18]+[（-18）+（-6.8）+（-3.2）]		B．	[（+6$\frac{1}{3}$）+（-6.8）+（+4$\frac{2}{3}$）]+[（-18）+18+（-3.2）]
	C．	[（+6$\frac{1}{3}$）+（-18）]+[（+4$\frac{2}{3}$）+（-6.8）]+[18+（-3.2）]		D．	[（+6$\frac{1}{3}$）+（+4$\frac{2}{3}$）]+[（-18）+18]+[（-3.2）+（-6.8）]

科目：初中数学 来源： 题型：选择题

3．计算π⁰，结果是（　　）

A．

B．

C．

D．

3.14

科目：初中数学 来源： 题型：解答题