
| A. | k=4a | B. | k=-4a | C. | k=-$\frac{a}{4}$ | D. | k=4a或k=-4a |
分析 把(3,0)代入二次函数的解析式求得t的值,则二次函数的解析式即可求得,代入y2=kx+b(b≠0)求得k和b的关系,则y即可利用a、k、b表示,然后根据函数y=y1+y2与x轴只有一个交点求得.
解答 解:把(3,0)代入抛物线y1=a(x-t)(x+t-2)(a≠0)得a(3-t)(1+t)=0,
∵a≠0,
∴t=3或-1.
则y1=a(x+1)(x-3),即y1=ax2-2ax-3a,
把(3,0)代入y=kx+b得3k+b=0,即b=-3a.
函数y=y1+y2=ax2-2ax-3a+(kx+b)=ax2+(k-2a)x+(b-3a).
则(k-2a)2-4a(b-3a)=k2+16a-4ak-4ab=k2+16a2-4ak+12ak=k2+16a2+8ak=(k+4a)2=0,
则k+4a=0,
则k=-4a.
故选B.
点评 本题考查了二次函数图象与x轴的交点的个数,根据求得t的值是解决本题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
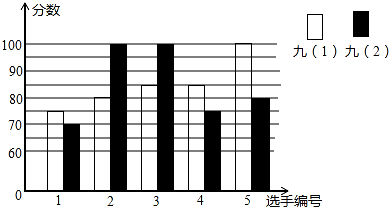 某中学开展某项比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为 100分)如图所示:
某中学开展某项比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为 100分)如图所示:| 班级 | 平均数(分) | 中位数(分) | 众数(分) | 方差 |
| 九(1) | 65 | 85 | 65 | 70 |
| 九(2) | 85 | 80 | 100 | 160 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com