
 在平面直角坐标系中,若横坐标、纵坐标均为整数点称为格点,若一个多边形的顶点都是格点,则称为格点多边形.记格点多边形的面积为S,其内部的格点数记为n,边界上的格点数记为l,例如图中△ABC是格点三角形,对应的S=1,n=0,l=4.奥地利数学家皮克发现格点多边形的面积可表示为S=n+al+b,其中a,b为常数.
在平面直角坐标系中,若横坐标、纵坐标均为整数点称为格点,若一个多边形的顶点都是格点,则称为格点多边形.记格点多边形的面积为S,其内部的格点数记为n,边界上的格点数记为l,例如图中△ABC是格点三角形,对应的S=1,n=0,l=4.奥地利数学家皮克发现格点多边形的面积可表示为S=n+al+b,其中a,b为常数.分析 (1)根据格点多边形的面积S=N+aL+b,结合图中的格点三角形ABC及格点四边形DEFG,建立方程组,求出a,b即可求得S;
(2)将n、l的值代入(1)中代数式求值即可;
(3)利用(1)中的函数关系式进行解答.
解答 解:(1)根据题意,可得:$\left\{\begin{array}{l}{4a+b=1}\\{1+6a+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-1}\end{array}\right.$,
∴S=n+$\frac{1}{2}$l-1;
(2)将n=20、l=15代入可得S=20+$\frac{1}{2}$×15-1=26.5;
(3)如图,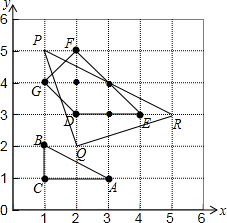 .
.
点评 此题考查格点图形的面积变化与多边形内部格点数和边界格点数的关系,从简单情况分析,找出规律解决问题.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 作图与证明:
作图与证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,DE⊥AB于点D,交AC于点E.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,DE⊥AB于点D,交AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com