Question

（1）用公式法解方程：x²-6x+1=0（2）用配方法解一元二次方程：x²+1=3x．

Answer 1

解：（1）∵方程x²-6x+1=0的二次项系数a=1，一次项系数b=-6，常数项c=1，
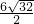
∴x===3±2，
∴x₁=3+2，x₂=3-2；

（2）由原方程，得
x²-3x=-1，
等式的两边同时加上一次项系数一半的平方，得
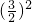
x²-3x+=-1+，
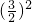
∴（x-）²=，
∴x=±，
∴x₁=，x₂=．
分析：（1）利用求根公式x=解方程；
（2）将常数项移到等式的右边，含有未知数的项移到等式的左边，然后在等式的两边同时加上一次项系数一半的平方，构成完全平方公式形式；最后直接开平方即可．
点评：本题考查了解一元二次方程--公式法、配方法．利用公式法解方程时，需熟记求根公式．