
(2013年四川攀枝花12分)如图,在平面直角坐标系中,四边形ABCD是梯形,AB∥CD,点B(10,0),C(7,4).直线l经过A,D两点,且sin∠DAB= .动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
.动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
(1)点A的坐标为 ,直线l的解析式为 ;
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围;
(3)试求(2)中当t为何值时,S的值最大,并求出S的最大值;
(4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
解:(1)(﹣4,0);y=x+4。
(2)在点P、Q运动的过程中:
①当0<t≤1时,如图1,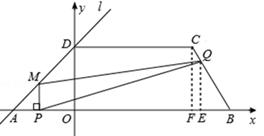
过点C作CF⊥x轴于点F,则CF=4,BF=3,由勾股定理得BC=5。
过点Q作QE⊥x轴于点E,则BE=BQ•cos∠CBF=5t•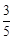 =3t。
=3t。
∴PE=PB﹣BE=(14﹣2t)﹣3t=14﹣5t,
S=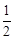 PM•PE=
PM•PE=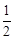 ×2t×(14﹣5t)=﹣5t2+14t。
×2t×(14﹣5t)=﹣5t2+14t。
②当1<t≤2时,如图2,
过点C、Q分别作x轴的垂线,垂足分别为F,E,则CQ=5t﹣5,PE=AF﹣AP﹣EF=11﹣2t﹣(5t﹣5)=16﹣7t。
S=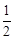 PM•PE=
PM•PE=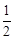 ×2t×(16﹣7t)=﹣7t2+16t。
×2t×(16﹣7t)=﹣7t2+16t。
③当点M与点Q相遇时,DM+CQ=CD=7,
即(2t﹣4)+(5t﹣5)=7,解得t=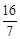 。
。
当2<t<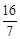 时,如图3,
时,如图3,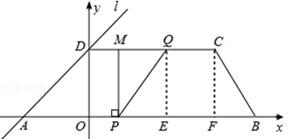
MQ=CD﹣DM﹣CQ=7﹣(2t﹣4)﹣(5t﹣5)=16﹣7t,
S=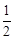 PM•MQ=
PM•MQ=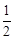 ×4×(16﹣7t)=﹣14t+32。
×4×(16﹣7t)=﹣14t+32。
综上所述,点Q与点M相遇前S与t的函数关系式为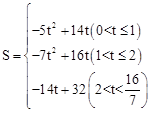 。
。
(3)①当0<t≤1时,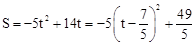 ,
,
∵a=﹣5<0,抛物线开口向下,对称轴为直线t=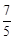 ,
,
∴当0<t≤1时,S随t的增大而增大。
∴当t=1时,S有最大值,最大值为9。
②当1<t≤2时,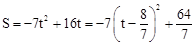 ,
,
∵a=﹣7<0,抛物线开口向下,对称轴为直线t=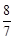 ,
,
∴当t=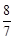 时,S有最大值,最大值为
时,S有最大值,最大值为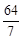 。
。
③当2<t<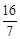 时,S=﹣14t+32
时,S=﹣14t+32
∵k=﹣14<0,∴S随t的增大而减小。
又∵当t=2时,S=4;当t=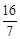 时,S=0,∴0<S<4。
时,S=0,∴0<S<4。
综上所述,当t=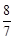 时,S有最大值,最大值为
时,S有最大值,最大值为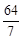 。
。
(4)t=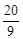 或t=
或t=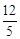 时,△QMN为等腰三角形。
时,△QMN为等腰三角形。
解析


科目:初中数学 来源: 题型:解答题
某物体从P点运动到Q点所用时间为7秒,其运动速度v(米每秒)关于时间t(秒)的函数关系如图所示.某学习小组经过探究发现:该物体前进3秒运动的路程在数值上等于矩形AODB的面积.由物理学知识还可知:该物体前n(3<n≤7)秒运动的路程在数值上等于矩形AODB的面积与梯形BDNM的面积之和.
根据以上信息,完成下列问题:
(1)当3<n≤7时,用含t的式子表示v;
(2)分别求该物体在0≤t≤3和3<n≤7时,运动的路程s(米)关于时间t(秒)的函数关系式;并求该物体从P点运动到Q总路程的 时所用的时间.
时所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
5月12日是母亲节,小明去花店买花送给母亲,挑中了象征温馨、母爱的康乃馨和象征高贵、尊敬的兰花两种花,已知康乃馨每支5元,兰花每支3元,小明只有30元,希望购买花的支数不少于7支,其中至少有一支是康乃馨.
(1)小明一共有多少种可能的购买方案?列出所有方案;
(2)如果小明先购买一张2元的祝福卡,再从(1)中任选一种方案购花,求他能实现购买愿望的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
周末,小明骑自行车从家里出发到野外郊游.从家出发1小时后到达南亚所(景点),游玩一段时间后按原速前往湖光岩.小明离家1小时50分钟,妈妈驾车沿相同路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.
(1)求小明骑车的速度和在南亚所游玩的时间;
(2)若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x; y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某游泳池有水4000m3,先放水清洗池子.同时,工作人员记录放水的时间x(单位:分钟)与池内水量y(单位:m3) 的对应变化的情况,如下表:
| 时间x(分钟) | … | 10 | 20 | 30 | 40 | … |
| 水量y(m3) | … | 3750 | 3500 | 3250 | 3000 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么,什么情况下到甲商场购买更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从O出发,沿x轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t(秒),下列能反映S与t之间函数关系的图象是( )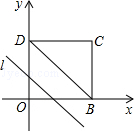
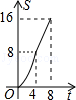
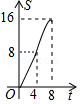


A B C D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com