
| 原料 含量 产品 | A(单位:千克) | B(单位:千克) |
| 甲 | 9 | 3 |
| 乙 | 4 | 10 |
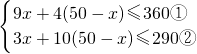 ,
,

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
| 原料 含量 产品 |
A(单位:千克) | B(单位:千克) |
| 甲 | 9 | 3 |
| 乙 | 4 | 10 |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏扬州市江都区八年级下学期期末考试数学试卷(带解析) 题型:解答题
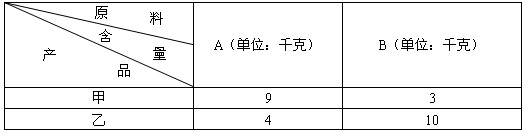
某公司为了开发新产品,用A、B两种原料各360千克、290千克,试制甲、乙两种新型产品共50件,下表是试验每件新产品所需原料的相关数据:
 | A(单位:千克) | B(单位:千克) |
| 甲 | 9 | 3 |
| 乙 | 4 | 10 |
查看答案和解析>>
科目:初中数学 来源:2013届江苏扬州市江都区八年级下学期期末考试数学试卷(解析版) 题型:解答题
某公司为了开发新产品,用A、B两种原料各360千克、290千克,试制甲、乙两种新型产品共50件,下表是试验每件新产品所需原料的相关数据:
|
|
A(单位:千克) |
B(单位:千克) |
|
甲 |
9 |
3 |
|
乙 |
4 |
10 |
(1)设生产甲种产品x件,根据题意列出不等式组,求出x的取值范围;
(2)若甲种产品每件成本为70元,乙种产品每件成本为90元,设两种产品的成本总额为y元,求出成本总额y(元)与甲种产品件数x(件)之间的函数关系式;当甲、乙两种产品各生产多少件时,产品的成本总额最少?并求出最少的成本总额.
查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com