
如图,直线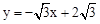 分别与x、y轴交于点B、C,点A(﹣2,0),P是直线BC上的动点.
分别与x、y轴交于点B、C,点A(﹣2,0),P是直线BC上的动点.
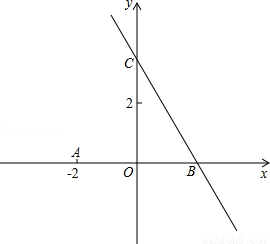
(1)求∠ABC的大小;
(2)求点P的坐标,使∠APO=30°;
(3)在坐标平面内,平移直线BC,试探索:当BC在不同位置时,使∠APO=30°的点P的个数是否保持不变?若不变,指出点P的个数有几个?若改变,指出点P的个数情况,并简要说明理由.
(1)60°
(2)点P坐标为(0,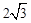 ),(1,
),(1,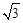 )
)
(3)当BC在不同位置时,点P的个数会发生改变,使∠APO=30°的点P的个数情况有四种:1个、2个、3个、4个。理由见解析
【解析】
试题分析:(1)求得B、C的坐标,在直角△BOC中,利用三角函数即可求解。
(2)取AC中点Q,以点Q为圆心,2为半径长画圆⊙Q,⊙Q与直线BC的两个交点,即为所求;
(3)当BC在不同位置时,点P的个数会发生改变,使∠APO=30°的点P的个数情况有四种:1个、2个、3个、4个,如答图2所示。
解:(1)在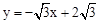 中,令x=0,得y=
中,令x=0,得y=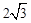 ;令y=0,得x=2。
;令y=0,得x=2。
∴C(0,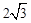 ),B(2,0)。∴OC=
),B(2,0)。∴OC=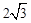 ,OB=2。
,OB=2。
∴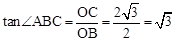 。∴∠ABC=60°。
。∴∠ABC=60°。
(2)如答图1,连接AC,
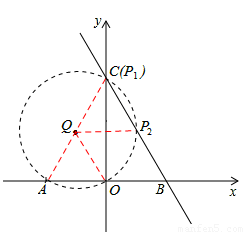
由(1)知∠ABC=60°,∴BC=2OB=4。
又∵AB=4,∴AB=BC。
∴△ABC为等边三角形,AB=BC=AC=4。
取AC中点Q,以点Q为圆心,2为半径长画圆,与直线BC交于点P1,P2。
∵QP1=2,QO=2,
∴点P1与点C重合,且⊙Q经过点O。
∴P1(0,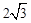 )。
)。
∵QA=QO,∠CAB=60°,∴△AOQ为等边三角形。
∴在⊙Q中,AO所对的圆心角∠OQA=60°。
由圆周角定理可知,AO所对的圆周角∠APO=30°,故点P1、P2符合条件。
∵QC=QP2,∠ACB=60°,∴△P2QC为等边三角形。∴P2C=QP=2。∴点P2为BC的中点。
∵B(2,0),C(0,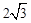 ),∴P2(1,
),∴P2(1,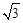 )。
)。
综上所述,符合条件的点P坐标为(0,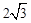 ),(1,
),(1,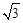 )。
)。
(3)当BC在不同位置时,点P的个数会发生改变,使∠APO=30°的点P的个数情况有四种:1个、2个、3个、4个。如答图2所示,

以AO为弦,AO所对的圆心角等于60°的圆共有2个,记为⊙Q,⊙Q′,点Q,Q′关于x轴对称。
∵直线BC与⊙Q,⊙Q′的公共点P都满足∠APO=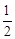 ∠AQO=
∠AQO=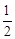 ∠AQ′O=30°,
∠AQ′O=30°,
∴点P的个数情况如下:
①有1个:直线BC与⊙Q(或⊙Q′)相切;
②有2个:直线BC与⊙Q(或⊙Q′)相交;
③有3个:直线BC与⊙Q(或⊙Q′)相切,同时与⊙Q(或⊙Q′)相交;直线BC过⊙Q与⊙Q′的一个交点,同时与两圆都相交;
④有4个:直线BC同时与两圆都相交,且不过两圆的交点


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
 已知:如图,直线y=-x+4分别与x轴,y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )
已知:如图,直线y=-x+4分别与x轴,y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )A、2
| ||
| B、6 | ||
C、3
| ||
D、4+2
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•青浦区二模)如图,直线y=x+1分别与 x轴、y轴分别相交于点A、B.抛物线y=ax2+bx+c(a≠0)与 y轴的正半轴相交于点C,与这个一次函数的图象相交于A、D,且sin∠ACB=
(2012•青浦区二模)如图,直线y=x+1分别与 x轴、y轴分别相交于点A、B.抛物线y=ax2+bx+c(a≠0)与 y轴的正半轴相交于点C,与这个一次函数的图象相交于A、D,且sin∠ACB=
| ||
| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线y=a分别与双曲线y=
如图,直线y=a分别与双曲线y=| 1 |
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省济宁市九年级(上)期中数学试卷(解析版) 题型:解答题
 x-3分别与y轴、x轴交于点A,B,抛物线y=-
x-3分别与y轴、x轴交于点A,B,抛物线y=- x2+2x+2与y轴交于点C,此抛物线的对称轴分别与BC,x轴交于点P,Q.
x2+2x+2与y轴交于点C,此抛物线的对称轴分别与BC,x轴交于点P,Q.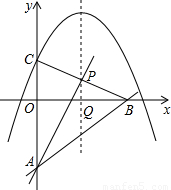
查看答案和解析>>
科目:初中数学 来源:2010-2011年山东肥城马埠中学初三模拟试题二数学卷 题型:选择题
已知:如图,直线 分别与
分别与 轴,
轴, 轴交于
轴交于 两点,从点
两点,从点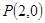 射出的光线经直线
射出的光线经直线 反射后再射到直线
反射后再射到直线 上,最后经直线
上,最后经直线 反射后又回到
反射后又回到 点,则光线所经过的路程是( )
点,则光线所经过的路程是( )
A.  B.
B.
 C.
C. D.
D. 

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com