
(本题满分12分)如图,过A(8,0)、B(0, )两点的直线与直线
)两点的直线与直线 交于点C.平行于
交于点C.平行于 轴的直线
轴的直线 从原点O出发,以每秒1个单位长度的速度沿
从原点O出发,以每秒1个单位长度的速度沿 轴向右平移,到C点时停止;
轴向右平移,到C点时停止; 分别交线段BC、OC于点D、E,以DE为边向左侧作等边△DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线
分别交线段BC、OC于点D、E,以DE为边向左侧作等边△DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线 的运动时间为t(秒).
的运动时间为t(秒).
(1)直接写出C点坐标和t的取值范围;
(2)求S与t的函数关系式;
(3)设直线 与
与 轴交于点P,是否存在这样的点P,使得以P、O、F为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
轴交于点P,是否存在这样的点P,使得以P、O、F为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.

(1)C(4,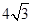 )
)
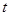 的取值范围是:0≤
的取值范围是:0≤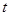 ≤4
≤4
(2)∵D点的坐标是(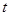 ,
, ),E的坐标是(
),E的坐标是(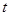 ,
,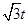 )
)
∴DE= -
-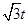 =
=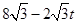 ……………………4分
……………………4分
∴等边△DEF的DE边上的高为:
∴当点F在BO边上时: =
=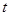 ,∴
,∴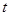 =3
……………………5分
=3
……………………5分
①
当0≤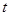 <3时,重叠部分为等腰梯形,可求梯形上底为:
<3时,重叠部分为等腰梯形,可求梯形上底为: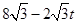 -
-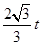 …7分
…7分
S=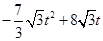
②
当3≤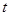 ≤4时,重叠部分为等边三角形
≤4时,重叠部分为等边三角形
S=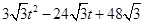
(3)存在,P(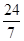 ,0)
,0)
【解析】(本题12
分)解(1)C(4,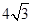 ) ……………………………2分
) ……………………………2分
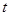 的取值范围是:0≤
的取值范围是:0≤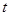 ≤4 ……………………………… 3分
≤4 ……………………………… 3分
(2)∵D点的坐标是(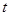 ,
, ),E的坐标是(
),E的坐标是(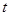 ,
,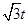 )
)
∴DE= -
-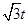 =
=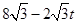 ……………………4分
……………………4分
∴等边△DEF的DE边上的高为:
∴当点F在BO边上时: =
=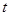 ,∴
,∴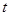 =3
……………………5分
=3
……………………5分

③
当0≤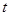 <3时,重叠部分为等腰梯形,可求梯形上底为:
<3时,重叠部分为等腰梯形,可求梯形上底为: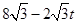 -
-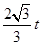 …7分
…7分
S=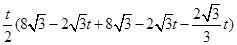
=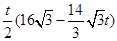
=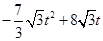 ………………………………8分
………………………………8分
④
当3≤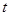 ≤4时,重叠部分为等边三角形
≤4时,重叠部分为等边三角形
S= ………………… 9分
………………… 9分
=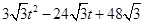 ……………………10分
……………………10分
(3)存在,P(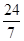 ,0) ……………………12分
,0) ……………………12分
说明:∵FO≥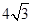 ,FP≥
,FP≥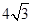 ,OP≤4
,OP≤4
∴以P,O,F以顶点的等腰三角形,腰只有可能是FO,FP,
若FO=FP时,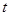 =2(12-3
=2(12-3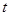 ),
),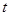 =
=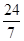 ,∴P(
,∴P(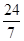 ,0)
,0)


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
(本题满分12分)
如图,直角梯形ABCD中,AB∥DC,![]() ,
,![]() ,
,![]() .动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).

(1)当![]() 时,求线段
时,求线段 的长;
的长;
(2)当0<t<2时,如果以C、P、Q为顶点的三角形为直角三角形,求t的值;
(3)当t>2时,连接PQ交线段AC于点R.请探究![]() 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(贵州铜仁卷)数学 题型:解答题
(本题满分12分)如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
 |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年上海市徐汇区中考一模数学卷 题型:解答题
(本题满分12分)
如图, 的顶点A、B在二次函数
的顶点A、B在二次函数 的图像上,又点A、B[来分别在
的图像上,又点A、B[来分别在 轴和
轴和 轴上,
轴上, ∠ABO=
∠ABO= .
.

1.(1)求此二次函数的解析式;(4分)
2.
|
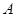 作
作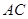 ∥
∥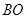 交上述函数图像于点
交上述函数图像于点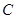 ,
,
点 在上述函数图像上,当
在上述函数图像上,当 与
与 相似时,求点
相似时,求点 的坐标.(8分)
的坐标.(8分)
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生考试数学卷(广东珠海) 题型:解答题
(本题满分12分)如图1,抛物线 与x轴交于A、C两点,与y轴交于B点,与直线
与x轴交于A、C两点,与y轴交于B点,与直线 交于A、D两点。
交于A、D两点。
⑴直接写出A、C两点坐标和直线AD的解析式;
⑵如图2,质地均匀的正四面体骰子的各个面上依次标有数字-1、1、3、4.随机抛掷这枚骰子两次,把第一次着地一面的数字m记做P点的横坐标,第二次着地一面的数字n记做P点的纵坐标.则点 落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?


查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(广西桂林) 题型:解答题
(本题满分12分)
如图,直角梯形ABCD中,AB∥DC, ,
, ,
, .动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).

(1)当 时,求线段
时,求线段 的长;
的长;
(2)当0<t<2时,如果以C、P、Q为顶点的三角形为直角三角形,求t的值;
(3)当t>2时,连接PQ交线段AC于点R.请探究 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com