
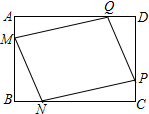
 某小区在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,为了绿化环境又节省成本.如图,已知矩形的边BC=200m,边AB=a m(a为不大于200的常数),四边形MNPQ的顶点在矩形的边上,且AM=BN=CP=DQ=x m,设四边形MNPQ的面积为S m2
某小区在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,为了绿化环境又节省成本.如图,已知矩形的边BC=200m,边AB=a m(a为不大于200的常数),四边形MNPQ的顶点在矩形的边上,且AM=BN=CP=DQ=x m,设四边形MNPQ的面积为S m2分析 (1)根据题意和图形可以得到S关于x的函数关系式和x的取值范围;
(2)根据a的值,将二次函数的一般形式化为顶点式,从而可以解答本题;
(3)根据a的值,将二次函数的一般形式化为顶点式,求出S的最小值,然后再乘以50,即可解答本题.
解答 解:(1)由题意可得,
S=200a-$\frac{x•(a-x)}{2}×2-\frac{(200-x)x}{2}×2$=2x2-(a+200)x+200a(0<x<a),
即S关于x的函数关系式是S=2x2-(a+200)x+200a,自变量x的取值范围是0<x<a;
(2)当a=120时,
S=2x2-320x+200×120=2(x-80)2+11200,
∴x=80时,S取得最小值,此时,S=11200,
即a=120,S的最小值是11200,此时x的值是80;
(3)当a=200时,
S=2x2-(200+200)x+200×200=2(x-100)2+20000,
∴当x=100时,S取得最小值,此时S=20000,
20000×50=1000000(元)=100(万元),
即此时绿化最低费用为100万元,
故答案为:100.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,求出相应的二次函数的最值,注意第三问中要化为万元.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com