
| PG | PC |

|
|
| 1 |
| 2 |
| 1 |
| 2 |
|

| 1 |
| 2 |
| PG |
| PC |
| 3 |


 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
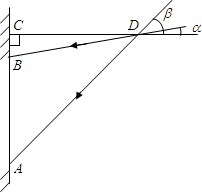 (2013•宝安区二模)在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)( )
(2013•宝安区二模)在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)( )查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•宝安区二模)如图,在矩形ABCD中,AB=3,BC=9,把矩形ABCD沿对角线BD折叠,使点C与点F重合,BF交AD于点M,过点C作CE⊥BF于点E,交AD于点G,则MG的长=
(2013•宝安区二模)如图,在矩形ABCD中,AB=3,BC=9,把矩形ABCD沿对角线BD折叠,使点C与点F重合,BF交AD于点M,过点C作CE⊥BF于点E,交AD于点G,则MG的长=| 11 |
| 4 |
| 11 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com