
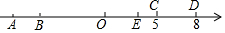 如图,数轴上有A、B、C、D、O五个点,点O为原点,点C在数轴上表示的数是5,线段CD的长度为3个单位,线段AB的长度为1个单位,且B、C两点之间的距离为12个单位,请解答下列问题:
如图,数轴上有A、B、C、D、O五个点,点O为原点,点C在数轴上表示的数是5,线段CD的长度为3个单位,线段AB的长度为1个单位,且B、C两点之间的距离为12个单位,请解答下列问题:分析 (1)结合图形以及点与点之间的距离即可找出点A、D表示的数;
(2)根据点E运动的规则即可找出点E在数轴上表示的数,利用两点间的距离公式即可找出关于t的一元一次方程,解之即可得出结论;
(3)分别找出运动时间为t时点A、B、P在数轴上表示的数,利用两点间的距离公式即可找出关于t的一元一次方程,解之即可得出结论.
解答 解:(1)∵点C在数轴上表示的数是5,线段CD的长度为3个单位,且点D在点C右侧,
∴点D在数轴上表示的数为8.
∵线段AB的长度为1个单位,且B、C两点之间的距离为12个单位,且点A在点B的左侧,点B在点C的左侧,
∴点B在数轴上表示的数为-7,点A在数轴上表示的数为-8.
故答案为:8;-8.
(2)点E在数轴上表示的数为2t-7,
∵CE的长度是2个单位,
∴|5-(2t-7)|=2,
解得:t=5或t=7.
∴点B的运动时间为5秒或7秒.
(3)∵点C在数轴上表示的数为5,点D在数轴上表示的数为8,点P为线段CD的中点,
∴点P在数轴上表示的数为$\frac{13}{2}$.
运动时间为t时,点A在数轴上表示的数为2t-8,点B在数轴上表示的数为2t-7,点P在数轴上表示的数为-4t+$\frac{13}{2}$,
当AP=$\frac{3}{2}$时,有|-4t+$\frac{13}{2}$-(2t-8)|=$\frac{3}{2}$,
解得:t=$\frac{13}{6}$或t=$\frac{8}{3}$;
当BP=$\frac{3}{2}$时,有|-4t+$\frac{13}{2}$-(2t-7)|=$\frac{3}{2}$,
解得:t=2或t=$\frac{5}{2}$.
综上所述:点P与线段AB的一个端点的距离为1.5个单位时运动的时间为2秒、$\frac{13}{6}$秒、$\frac{5}{2}$秒或$\frac{8}{3}$秒.
点评 本题考查了两点间的距离以及数轴,牢记两点间的距离是解题的关键.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
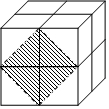 如图,这是由8个同样大小的立方体组成的魔方,体积为8cm3.
如图,这是由8个同样大小的立方体组成的魔方,体积为8cm3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
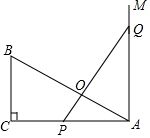 如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.
如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
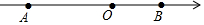 如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.
如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
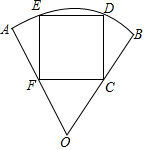 要在半径长为1米、圆心角为60°的扇形铁皮(如图)上截取一块面积尽可能大的正方形,请你设计一个截取方案(画出示意图),并计算这个正方形铁皮的面积(精确到0.01).
要在半径长为1米、圆心角为60°的扇形铁皮(如图)上截取一块面积尽可能大的正方形,请你设计一个截取方案(画出示意图),并计算这个正方形铁皮的面积(精确到0.01).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com