练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    下列说法错误的是（　　）
    A、等腰三角形底边上的高所在的直线是对称轴
    B、等腰三角形底边上的中线所在的直线是对称轴
    C、等腰三角形顶角的平分线所在的直线是对称轴
    D、等腰三角形一内角平分线所在的直线是对称轴
    考点：等腰三角形的性质,轴对称的性质
    专题：
    分析：根据等腰三角形和轴对称的性质分别判断后即可确定正确的选项．
    解答：解：A、等腰三角形底边上的高所在的直线是对称轴，正确；
    B、等腰三角形底边上的中线所在的直线是对称轴，正确；
    C、等腰三角形顶角的平分线所在的直线是对称轴，正确；
    D、等腰三角形一内角平分线所在的直线是对称轴，错误．
    故选D．
    点评：本题考查了等腰三角形的性质及轴对称的性质，属于基础题，解题的关键是了解对称轴是一条直线，难度不大．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

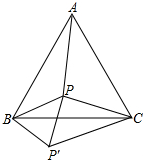    已知，P为等边三角形内一点，且BP=3，PC=4，将BP绕点B顺时针旋转60°至BP′的位置．
    （1）试判断△BPP′的形状，并说明理由；
    （2）若P′C=5，求PA．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

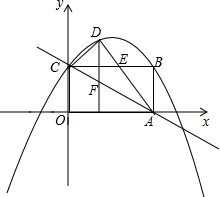    已知一个矩形纸片OABC，将该纸片放置在平面直角坐标系中，如图，点A（5，0），从（0，
    5
    2
    ），把矩形纸片沿对角线AC折叠，使点O落在点D，AD、BC相交于点E．
    （1）求CE的长；
    （2）求直线AC的函数解析式及点D的坐标；
    （3）求经过点C、D、B抛物线的解析式；
    （4）过点D作x轴的垂线，交直线AC于点F，点P是抛物线上的任意一点，过点P作x轴的垂线，交直线AC于点Q在抛物线上是否存在点P，使以点P、D、F、Q为顶点的四边形是平行四边形？若存在，求出点P的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，圆柱高12，底面半径3，一只蚂蚁从A点爬到B点去吃食，要爬行的最短路程是
     
    （π取3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

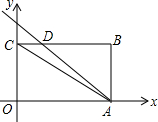    如图所示，在平面直角坐标系中，矩形OABC的对角线AC=10，OA、OC是方程x2-2（k+3）+12k=0的两根，且OA＞OC，点D在BC上，直线l平分矩形OABC的面积．
    （1）若S△ACD=6时，求D点坐标；
    （2）若直线l经过点D，求直线l的解析式；
    （3）是否存在直线l，使l与坐标轴围成的三角形与△ABD相似？如果存在，直接写出直线l的解析式；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下表中有两种移动电话计费方式．
      月使用费/元 主叫限定时间/min主叫超时费/（元/min）  被叫
     方式一 58 150 0.25 免费
     方式二 88350  0.19免费 
    设一个月内用移动电话主叫为t min（t是正整数），你能从中发现如何根据主叫时间选择省钱的计费方式吗？当t满足
     
    时，选择方式一，当t满足
     
    时，选择方式二．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知在△ABC中，∠A=90°，AB=AC，CD平分∠ACB，DE⊥BC于E，若BC=15，求△DEB的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知x1和x2是一元二次方程2x2-3x-4=0的两个实数根，那么x1+x2=
     
    ，x1•x2=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，矩形ABCD中，AB=4，BC=2，点B、D在⊙O上，O在AB上，CD交⊙O于E，则CE的长为
     
    ．

    查看答案和解析>>

    同步练习册答案