D
分析:连OA,OB,AD,DF,过A作AG⊥CF于G点,由AB=OA=OB=1,得到∠AOB=60°,弧AB的度数=60°,而AB=BC=CD,得弧ABD的度数=3×60°=180°,所以AD为⊙O的直径,∠CFA=60°;再由AE=DE,得OE垂直平分AD,AE=AF,得AD垂直平分EF,可得EF过O点,
弧FD=弧FA,得到△FAD为等腰直角三角形,可得FA=

AD=

,在Rt△AGF中,GF=

AF=

,AG=

GF=

,在Rt△AGC中,CG=AG=

,最后利用三角形的面积公式即可求出△ACF面积.
解答:

解:连OA,OB,AD,DF,过A作AG⊥CF于G点,如图,
∵AB=OA=OB=1,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴弧AB的度数=60°,
又∵AB=BC=CD,
∴弧AB=弧BC=弧CD,
∴弧ABD的度数=3×60°=180°,
∴AD为⊙O的直径,∠CFA=60°,
又∵AE=DE,
∴OE垂直平分AD,
∵AE=AF,
∴AD垂直平分EF,
∴EF过O点,
∴弧FD=弧FA,
∴△FAD为等腰直角三角形,
∴∠FCA=∠FDA=45°,FA=

AD=

,
在Rt△AGF中,GF=

AF=

,AG=

GF=

,
在Rt△AGC中,CG=AG=

,
∴S
△ACF=

CF•AG=

×(

+

)×

=
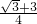
.
故选D.
点评:本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.也考查了等腰直角三角形的性质和含30度的直角三角形三边的关系以及三角形的面积公式.

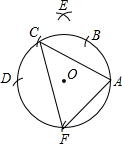 如图,在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD,分别以A、D为圆心A到C的距离为半径画弧,两弧交于E,以A为圆心O到E的距离为半径画弧,交⊙O于F.则△ACF面积是
如图,在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD,分别以A、D为圆心A到C的距离为半径画弧,两弧交于E,以A为圆心O到E的距离为半径画弧,交⊙O于F.则△ACF面积是

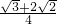
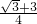
 AD=
AD= ,在Rt△AGF中,GF=
,在Rt△AGF中,GF= AF=
AF= ,AG=
,AG= GF=
GF= ,在Rt△AGC中,CG=AG=
,在Rt△AGC中,CG=AG= ,最后利用三角形的面积公式即可求出△ACF面积.
,最后利用三角形的面积公式即可求出△ACF面积. 解:连OA,OB,AD,DF,过A作AG⊥CF于G点,如图,
解:连OA,OB,AD,DF,过A作AG⊥CF于G点,如图, AD=
AD= ,
, AF=
AF= ,AG=
,AG= GF=
GF= ,
, ,
, CF•AG=
CF•AG= ×(
×( +
+ )×
)× =
=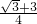 .
.

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案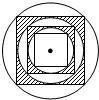 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( ) (2013•上海模拟)如图,在半径为1的扇形AOB中,∠AOB=90°,点P是
(2013•上海模拟)如图,在半径为1的扇形AOB中,∠AOB=90°,点P是