
(2013年四川攀枝花8分)如图,PA为⊙O的切线,A为切点,直线PO交⊙O与点E,F过点A作PO的垂线AB垂足为D,交⊙O与点B,延长BO与⊙O交与点C,连接AC,BF.

(1)求证:PB与⊙O相切;
(2)试探究线段EF,OD,OP之间的数量关系,并加以证明;
(3)若AC=12,tan∠F= ,求cos∠ACB的值.
,求cos∠ACB的值.
解:(1)证明:连接OA,
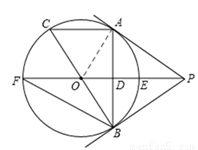
∵PA与⊙O相切,
∴PA⊥OA,即∠OAP=90°。
∵OP⊥AB,∴D为AB中点,即OP垂直平分AB
∴PA=PB。
∵在△OAP和△OBP中, ,
,
∴△OAP≌△OBP(SSS)。
∴∠OAP=∠OBP=90°。∴BP⊥OB。
∵OB是⊙O的半径,∴PB为圆O的切线。
(2)EF2=4DO•PO。证明如下:
∵∠OAP=∠ADO=90°,∠AOD=∠POA,∴△OAD∽△OPA。
∴ ,即OA2=OD•OP。
,即OA2=OD•OP。
∵EF为圆的直径,即EF=2OA,∴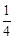 EF2=OD•OP,即EF2=4OD•OP。
EF2=OD•OP,即EF2=4OD•OP。
(3)连接BE,则∠FBE=90°。

∵tan∠F=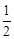 ,∴
,∴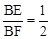 。∴可设BE=x,BF=2x。
。∴可设BE=x,BF=2x。
则由勾股定理,得 。
。
∵S△BEF=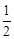 BE•BF=
BE•BF=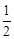 EF•BD,∴BD=
EF•BD,∴BD=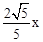 。
。
又∵AB⊥EF,∴AB=2BD= 。
。
∴Rt△ABC中,BC= ,AC2+AB2=BC2,
,AC2+AB2=BC2,
∴122+( )2=(
)2=( )2,解得:x=
)2,解得:x= 。
。
∴BC=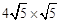 =20。
=20。
∴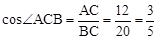 。
。
【解析】(1)连接OA,由OP垂直于AB,利用垂径定理得到D为AB的中点,即OP垂直平分AB,可得出AP=BP,再由OA=OB,OP=OP,利用SSS得出三角形AOP与三角形BOP全等,由PA为圆的切线,得到OA垂直于AP,利用全等三角形的对应角相等及垂直的定义得到OB垂直于BP,即PB为圆O的切线。
(2)由一对直角相等,一对公共角,得出三角形AOD与三角形OAP相似,由相似得比例,列出关系式,由OA为EF的一半,等量代换即可得证。
(3)连接BE,构建直角△BEF.在该直角三角形中利用锐角三角函数的定义、勾股定理可设BE=x,BF=2x,进而可得EF= ;然后由面积法求得
;然后由面积法求得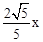 ,所以根据垂径定理求得AB的长度,在Rt△ABC中,根据勾股定理易求BC的长;最后由余弦三角函数的定义求解。
,所以根据垂径定理求得AB的长度,在Rt△ABC中,根据勾股定理易求BC的长;最后由余弦三角函数的定义求解。
考点:圆的综合题,切线的判定和性质,圆周角定理,垂径定理,全等三角形的判定和性质,相似三角形的判定和性质,锐角三角函数定义,勾股定理,三角形面积法的应用。


科目:初中数学 来源:2013年初中毕业升学考试(四川攀枝花卷)数学(解析版) 题型:填空题
(2013年四川攀枝花4分)某次数学测验中,某班六位同学的成绩分别是:86,79,81,86,90,84,这组数据的众数是 ,中位数是 .
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川攀枝花卷)数学(解析版) 题型:选择题
(2013年四川攀枝花3分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则函数 与y=bx+c在同一直角坐标系内的大致图象是【
】
与y=bx+c在同一直角坐标系内的大致图象是【
】
 A.
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川攀枝花卷)数学(解析版) 题型:选择题
(2013年四川攀枝花3分)已知实数x,y,m满足 ,且y为负数,则m的取值范围是【 】
,且y为负数,则m的取值范围是【 】
A.m>6 B.m<6 C.m>﹣6 D.m<﹣6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com