【答案】
分析:观察方程可得最简公分母是:x(x+1)(x+2)(x+3)(x+4),两边同时乘最简公分母可把分式方程化为整式方程来解答.
解答:解:方程两边同乘x(x+1)(x+2)(x+3)(x+4),得
(x+2)(x+3)(x+4)+x(x+3)(x+4)+x(x+1)(x+4)+x(x+1)(x+2)=
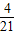
x(x+1)(x+2)(x+3)(x+4),
∴(x+3)(x+4)(2x+2)+x(x+1)(2x+6)=
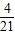
x(x+1)(x+2)(x+3)(x+4),
∴2(x+1)(x+3)(2x+4)=
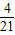
x(x+1)(x+2)(x+3)(x+4),
∴(x+1)(x+2)(x+3)[4-
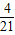
x(x+4)]=0,
∴x
1=-1,x
2=-2,x
3=-3,x
4=-7,x
5=3.
经检验:x
1=-1,x
2=-2,x
3=-3不是原方程的解,x
4=-7,x
5=3是原方程的解.
故原方程的解为x
1=-7,x
2=3.
故答案为x
1=-7,x
2=3.
点评:本题考查了分式方程的解法.解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.注意解分式方程一定要验根.本题去分母将原方程转化的整式方程是一元高次方程,所以运用因式分解法解此整式方程是解题的关键.本题题型只在竞赛题中出现,有一定难度.

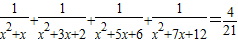 得 .
得 . 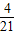 x(x+1)(x+2)(x+3)(x+4),
x(x+1)(x+2)(x+3)(x+4),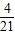 x(x+1)(x+2)(x+3)(x+4),
x(x+1)(x+2)(x+3)(x+4),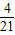 x(x+1)(x+2)(x+3)(x+4),
x(x+1)(x+2)(x+3)(x+4),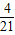 x(x+4)]=0,
x(x+4)]=0,

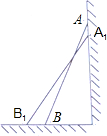 子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?