
 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).分析 (1)根据勾股定理AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5cm.根据相似三角形的性质得到结论;
(2)过点P作PH⊥BC于点H,作PF⊥AC于点F,则PH∥AC,PF∥BC.根据平行线分线段成比例定理得到PH=$\frac{8}{5}$t,同理BH=$\frac{6}{5}$t,于是求得PF=CH=3-$\frac{6}{5}t$,分别计算出S△PBN,S△APMS△CMN根据三角形面积的和差即可得到y与t之间的函数关系式是 y=-$\frac{3}{10}{t}^{2}+\frac{3}{2}t$;
(3)假设存在某一时刻t,使△PMN的面积是Rt△ABC面积的$\frac{1}{5}$,列方程得到取t=1;
(4)以A,P,M为顶点的三角形与△ABC相似,分两种情况:①△AMP∽△ABC;②△APM∽△ABC.列比例式求得t=$\frac{3}{2}$,此时CN=CM=$\frac{3}{2}$,过点P作PQ⊥BC于点Q,根据相似三角形的性质得到PQ=$\frac{12}{5}$,BQ=$\frac{9}{5}$,在△PMN中,PM2+MN2=$\frac{9}{4}+\frac{18}{4}=\frac{27}{4}$≠PN2,由勾股定理的逆定理可知,△PMN不是直角三角形.
解答 解:(1)如图,∵在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.
∴根据勾股定理,得AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5cm.
当PN⊥BC时,Rt△PBN∽Rt△ABC
此时$\frac{BP}{BA}=\frac{BN}{BC}$,即$\frac{2t}{5}=\frac{3-t}{3}$,解得t=$\frac{15}{11}$,
答:当t=$\frac{15}{11}$s时,PN⊥BC;
(2)过点P作PH⊥BC于点H,作PF⊥AC于点F,则PH∥AC,PF∥BC.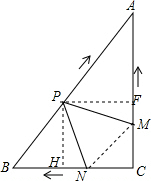
∴$\frac{PH}{AC}=\frac{BP}{BA}$,即$\frac{PH}{4}=\frac{2t}{5}$,
∴PH=$\frac{8}{5}$t,
同理BH=$\frac{6}{5}$t,
∴PF=CH=3-$\frac{6}{5}t$,
S△PBN=$\frac{1}{2}$(3-t)$\frac{8}{5}$t=$\frac{12}{5}t-\frac{4}{5}{t}^{2}$,
S△APM=$\frac{1}{2}$(4-t)(3-$\frac{6}{5}t$)=$\frac{3}{5}{t}^{2}-\frac{39}{10}t+6$
S△CMN=$\frac{1}{2}$•t•t=$\frac{1}{2}$t2,
∴y=S△ABC-S△PBN-S△PAM-S△CMN
=6-($\frac{12}{5}t-\frac{4}{5}{t}^{2}$)-($\frac{3}{5}{t}^{2}-\frac{39}{10}t+6$)-$\frac{1}{2}$t2
=-$\frac{3}{10}{t}^{2}+\frac{3}{2}t$,
答:y与t之间的函数关系式是 y=-$\frac{3}{10}{t}^{2}+\frac{3}{2}t$;
(3)假设存在某一时刻t,使△PMN的面积是Rt△ABC面积的$\frac{1}{5}$,
此时-$\frac{3}{10}{t}^{2}+\frac{3}{2}t$=$\frac{1}{5}$•6
解方程得t1=1,t2=4,
∵0<t<2.5,
∴t2=4不合题意,舍去,取t=11,
答:当t=1时,△PMN的面积是Rt△ABC面积的$\frac{1}{5}$;
(4)以A,P,M为顶点的三角形与△ABC相似,分两种情况:
①当△AMP∽△ABC时,$\frac{AP}{AC}=\frac{AM}{AB}$,即$\frac{5-2t}{4}=\frac{4-t}{5}$,
解得t=$\frac{3}{2}$;
②当△APM∽△ABC时,$\frac{AM}{AC}=\frac{AP}{AB}$,即$\frac{4-t}{4}=\frac{5-2t}{5}$,
解得t=0(不合题意,舍去);
综上所述,当t=$\frac{3}{2}$时,以A、P、M为顶点的三角形与△ABC相似,
此时CN=CM=$\frac{3}{2}$,∴MN=$\frac{3}{2}$$\sqrt{2}$,
AM=$\frac{5}{2}$,AP=2,PM=$\frac{3}{2}$,
过点P作PQ⊥BC于点Q,
由△PBQ∽△ABC,得PQ=$\frac{12}{5}$,BQ=$\frac{9}{5}$,
∴NQ=BQ-BN=$\frac{9}{5}$-$\frac{3}{2}$=$\frac{3}{10}$,
∴PN2=NQ2+PQ2=$\frac{585}{100}=\frac{117}{20}$,
在△PMN中,PM2+MN2=$\frac{9}{4}+\frac{18}{4}=\frac{27}{4}$≠PN2,
∴由勾股定理的逆定理可知,△PMN不是直角三角形.
点评 本题综合考查的是相似形综合题,涉及到相似三角形的判定与性质、平行线分线段成比例,二次函数最值的求法以及三角形面积公式.利用相似三角形的对应边成比例解题时,务必找准对应边.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 组员 | 甲 | 乙 | 丙 | 丁 | 戊 | 平均成绩 |
| 成绩 | 91 | 89 | ★ | 90 | 92 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 300 | B. | 310 | C. | 600 | D. | 620 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
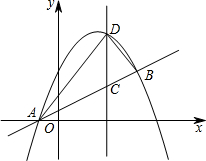 如图,抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
如图,抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 22或25 | B. | 25 | C. | 22 | D. | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com