
 半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2
半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2 ,且MN在正方形的对角线BD上,则正方形的边长为________.
,且MN在正方形的对角线BD上,则正方形的边长为________.
 解:①当圆心O在对角线BD的上方时,
解:①当圆心O在对角线BD的上方时, OQ=2
OQ=2 ,
, ,
, +1,
+1,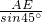 =
= AE=4+2
AE=4+2 ,
, -1,
-1,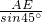 =
= AE=4-2
AE=4-2
 或4-2
或4-2 .
.

科目:初中数学 来源: 题型:
| 3 |
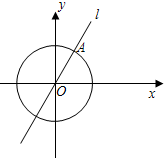 O相交于点A.
O相交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 | 4 |
 .5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间?
.5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间?查看答案和解析>>
科目:初中数学 来源: 题型:
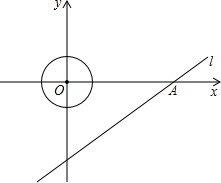
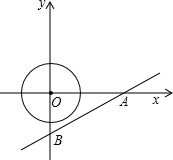 如图,直线l的解析式为y=
如图,直线l的解析式为y=| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 Q分别为PB、弧CQB上的切点.
Q分别为PB、弧CQB上的切点.查看答案和解析>>
科目:初中数学 来源: 题型:
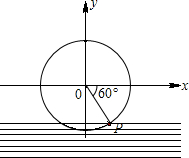 如图,半径为4m的水车圆O放在坐标系xOy中,已知水车每分钟按逆时针方向转1圈,如果水车上点P从浮出水时开始计算时间,此时OP与x轴正方向夹角为60°,则当水车转15秒时,点P上升的高度为
如图,半径为4m的水车圆O放在坐标系xOy中,已知水车每分钟按逆时针方向转1圈,如果水车上点P从浮出水时开始计算时间,此时OP与x轴正方向夹角为60°,则当水车转15秒时,点P上升的高度为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com