
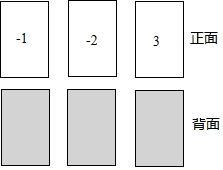
 有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b
有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b分析 (1)利用概率的计算方法解答;
(2)画出树状图,共有6种情况,其中满足一次函数y=kx+b经过第一、二、四象限的结果有2个,求出概率即可.
解答 解:(1)∵共有3张牌,两张为负数,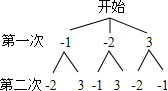
∴k为负数的概率是$\frac{2}{3}$;
(2)画树状图:
共有6种情况,其中满足一次函数y=kx+b经过第一、二、四象限,
即k<0,b>0的情况有2种,
所以一次函数y=kx+b经过第一、二、四象限的概率为$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题考查了用树状图或列表法、概率公式、一次函数的图象;一次函数y=kx+b的图象与系数的关系;熟练掌握树状图法是解决问题的关键.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
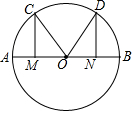 如图,已知AB为圆O的直径,M,N分别为OA,OB的中点,CM⊥AB,DN⊥AB,垂足分别为M,N,连结OC,OD,求证:$\widehat{AC}$=$\widehat{BD}$.
如图,已知AB为圆O的直径,M,N分别为OA,OB的中点,CM⊥AB,DN⊥AB,垂足分别为M,N,连结OC,OD,求证:$\widehat{AC}$=$\widehat{BD}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠BAC=∠BEF=90°,AB=AC=3,EB=EF,BF=1,O为FC的中点,当△EBF绕点B旋转(在△ABC所在平面内)时,AO的最大值为$\frac{3\sqrt{2}+1}{2}$.
如图,∠BAC=∠BEF=90°,AB=AC=3,EB=EF,BF=1,O为FC的中点,当△EBF绕点B旋转(在△ABC所在平面内)时,AO的最大值为$\frac{3\sqrt{2}+1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
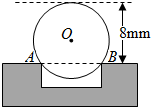 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示.
工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com