
【题目】如图,在平面直角坐标系 xOy 中,直线 y ![]() x 4与 x 轴、y 轴分别交于点 A、点 B,点 D 在 y 轴的负半轴上,若将△DAB 沿着直线 AD 折叠,点 B 恰好落在 x 轴正半轴上的点 C处.
x 4与 x 轴、y 轴分别交于点 A、点 B,点 D 在 y 轴的负半轴上,若将△DAB 沿着直线 AD 折叠,点 B 恰好落在 x 轴正半轴上的点 C处.
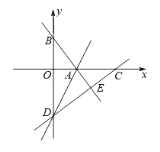
(1)求直线 CD 的表达式;
(2)在直线 AB 上是否存在一点 P,使得 SPCD![]() SOCD?若存在,直接写出点 P 的坐标;若不存在,请说明理由.
SOCD?若存在,直接写出点 P 的坐标;若不存在,请说明理由.
【答案】(1)![]() .(2) 存在一点P为P1(
.(2) 存在一点P为P1(![]() ,
,![]() ),P2(12,-12).
),P2(12,-12).
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A,B的坐标,在Rt△AOB中,利用勾股定理可求出AB的长度,由折叠的性质可得出AC=AB,结合OC=OA+AC可得出OC的长度,进而可得出点C的坐标,设OD=x,则CD=DB=x+4.,Rt△OCD中,依据勾股定理可求得x的值,从而可得到点D(0,-6),然后利用待定系数法求解即可;
(2)假设存在,设点P的坐标为(m, ![]() m 4),则F(m,
m 4),则F(m, ![]() m-6),PF=
m-6),PF=![]() 利用三角形的面积公式可得出关于m的含绝对值符号的一元一次方程,解之即可得出结论.
利用三角形的面积公式可得出关于m的含绝对值符号的一元一次方程,解之即可得出结论.
解:(1)令x=0得:y=4,
∴B(0,4).
∴OB=4
令y=0得:0=-![]() x+4,解得:x=3,
x+4,解得:x=3,
∴A(3,0).
∴OA=3.
在Rt△OAB中,AB=![]() .
.
∴OC=OA+AC=3+5=8,
∴C(8,0).设OD=x,则CD=DB=x+4.
在Rt△OCD中,DC2=OD2+OC2,即(x+4)2=x2+82,解得:x=6,
∴D(0,-6).
设CD的解析式为y=kx-6,将C(8,0)代入得:8k-6=0,解得:k=![]() ,
,
∴直线CD的解析式为y=![]() x-6.
x-6.

(2)过点P作PF∥y轴交CD于F, ∵P点在直线BA上,设P(m, ![]() m 4),则F(m,
m 4),则F(m, ![]() m-6), ∴PF=
m-6), ∴PF=![]() =
=![]() , ∵
, ∵![]() ,D(0,-6),C(8,0),∴
,D(0,-6),C(8,0),∴![]()
![]() ×8=
×8=![]() ×8×6×
×8×6×![]() =60,解得:m=-
=60,解得:m=-![]() 或m=12, ∴
或m=12, ∴![]() (-
(-![]() ,
,![]() ),
),![]() (12,-12),
(12,-12),
综上所述,在直线 AB 上存在一点 P为![]() (-
(-![]() ,
,![]() ),
),![]() (12,-12).
(12,-12).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=![]() x+m的图象与x轴交于点A(﹣4,0),与二次函数y=ax2+bx+c的图象交于y轴上一点B,该二次函数的顶点C在x轴上,且OC=2.
x+m的图象与x轴交于点A(﹣4,0),与二次函数y=ax2+bx+c的图象交于y轴上一点B,该二次函数的顶点C在x轴上,且OC=2.
(1)求点B坐标;
(2)求二次函数y=ax2+bx+c的解析式;
(3)设一次函数y=![]() x+m的图象与二次函数y=ax2+bx+c的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD是以BD为直角边的直角三角形,求点P的坐标.
x+m的图象与二次函数y=ax2+bx+c的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD是以BD为直角边的直角三角形,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD,点 E,F 分别在 AD,CD 上,且DE=CF,AF 与 BE 相交于点G.
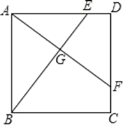
(1)求证:AF⊥BE;
(2)若 AB=6,DE=2,AG的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交与点D.
(1)判断CD与⊙O的位置关系并说明理由;
(2)若∠ACB=120°,OA=2,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大双,小双的妈妈申购到一张北京奥运会的门票,兄弟俩决定分别用标有数字且除数字以外没有其它任何区别的小球,各自设计一种游戏确定谁去.
大双:A袋中放着分别标有数字1,2,3的三个小球,B袋中放着分别标有数字4,5的两个小球,且都已各自搅匀,小双蒙上眼睛从两个口袋中各取出1个小球,若两个小球上的数字之积为偶数,则大双得到门票;若积为奇数,则小双得到门票.
小双:口袋中放着分别标有数字1,2,3的三个小球,且已搅匀,大双,小双各蒙上眼睛有放回地摸1次,大双摸到偶数就记2分,摸到奇数记0分;小双摸到奇数就记1分,摸到偶数记0分,积分多的就得到门票.(若积分相同,则重复第二次.)
(1)大双设计的游戏方案对双方是否公平?请你运用列表或树状图说明理由;
(2)小双设计的游戏方案对双方是否公平?不必说理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.

【答案】(1)证明见解析;(2)112.5°.
【解析】试题分析: ![]() 根据同角的余角相等可得到
根据同角的余角相等可得到![]() 结合条件
结合条件![]() ,再加上
,再加上![]() 可证得结论;
可证得结论;![]() 根据
根据![]() 得到
得到![]() 根据等腰三角形的性质得到
根据等腰三角形的性质得到![]() 由平角的定义得到
由平角的定义得到![]()
试题解析: ![]() 证明:
证明:

![]()
![]()
![]()
在△ABC和△DEC中,  ,
,
![]()
![]()
(2)∵∠ACD=90°,AC=CD,
∴∠1=∠D=45°,
∵AE=AC,
∴∠3=∠5=67.5°,
∴∠DEC=180°-∠5=112.5°.
【题型】解答题
【结束】
21
【题目】一个零件的形状如图所示,工人师傅按规定做得∠B=90°,
AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com