
分析 (1)先求出判别式△的值,再根据“△”的意义证明即可;
(2)根据根与系数的关系得出x1+x2=m+3,x1•x2=3m,根据勾股定理可知x12+x22=10,利用完全平方公式得出关于m的方程,求出方程的解即可.
解答 (1)证明:△=[-(m+3)]2-4×3m=m2-6m+9=(m-3)2,
因为不论m为何值,(m-3)2≥0,
所以△≥0,
所以无论m取什么实数值,该方程总有两个实数根;
(2)解:根据根与系数的关系得:x1+x2=m+3,x1•x2=3m,
∵该方程的两实根x1和x2是一个矩形两邻边的长且该矩形的对角线长为$\sqrt{10}$,
∴x12+x22=10,
∴x12+x22=(x1+x2)2-2•x1•x2=(m+3)2-2•3m=10,
即m2=1,
解得:m1=1,m2=-1(舍去),
即m的值为1.
点评 本题考查了根与系数的关系和根的判别式的应用,能正确运用性质进行计算是解此题的关键,题目比较好,难度适中.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
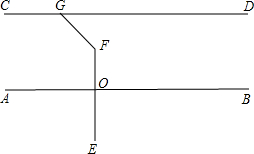 如图:已知AB∥CD,EF⊥AB于点O,∠FGC=131°,求∠EFG的度数.
如图:已知AB∥CD,EF⊥AB于点O,∠FGC=131°,求∠EFG的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
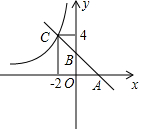 如图,一条直线分别交x轴、y轴于A、B两点,交反比例函数y=$\frac{m}{x}$(m≠0)位于第二象限的一支于C点,OA=OB=2.
如图,一条直线分别交x轴、y轴于A、B两点,交反比例函数y=$\frac{m}{x}$(m≠0)位于第二象限的一支于C点,OA=OB=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
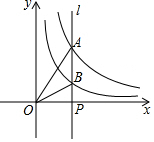 如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{5}{x}$(x>0)及y2=$\frac{k}{x}$(x>0)的图象分别交于A、B,若△AOB的面积为2,则k=1.
如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{5}{x}$(x>0)及y2=$\frac{k}{x}$(x>0)的图象分别交于A、B,若△AOB的面积为2,则k=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com