
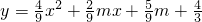 与x轴交于A,B两点,已知点A在x轴的负半轴上,点B在x轴的正半轴上,且BO=2AO,点C为抛物线的顶点.
与x轴交于A,B两点,已知点A在x轴的负半轴上,点B在x轴的正半轴上,且BO=2AO,点C为抛物线的顶点.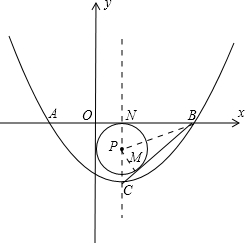 解:(1)设A点的坐标为(-a,0),则B点的坐标为(2a,0),其中a>0.
解:(1)设A点的坐标为(-a,0),则B点的坐标为(2a,0),其中a>0.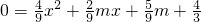 ,
,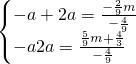 ?2m2-5m-12=0,
?2m2-5m-12=0, (不合题意舍去),
(不合题意舍去),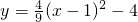 ,
, ,
, ;
;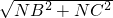 =
= =5,
=5,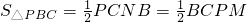 ,
, ,
,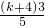 ,
, ,
, .
.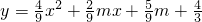 与x轴交于A,B两点,且A在x轴的负半轴上,点B在x轴的正半轴上,且BO=2AO.故设A点的坐标为(-a,0),则B点的坐标为(2a,0),其中a>0.令y=0,那么抛物线的解析式就变成关于x的一元二次方程的解,两个解分别是-a、2a.利用根与系数的关系写出
与x轴交于A,B两点,且A在x轴的负半轴上,点B在x轴的正半轴上,且BO=2AO.故设A点的坐标为(-a,0),则B点的坐标为(2a,0),其中a>0.令y=0,那么抛物线的解析式就变成关于x的一元二次方程的解,两个解分别是-a、2a.利用根与系数的关系写出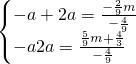 ,解得a、m的值.抛物线解析式确定,并写出顶点式,C点的坐标值即可确定.根据两点B、C的坐标值,求出直线BC的解析式.
,解得a、m的值.抛物线解析式确定,并写出顶点式,C点的坐标值即可确定.根据两点B、C的坐标值,求出直线BC的解析式.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
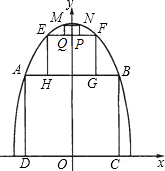 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:查看答案和解析>>
科目:初中数学 来源: 题型:
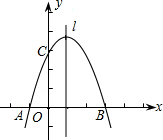 ,B,C三点的抛物的对称轴为直线l,D为对称轴l上一动点.
,B,C三点的抛物的对称轴为直线l,D为对称轴l上一动点.查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(32):2.3 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(52):2.8 二次函数的应用(解析版) 题型:解答题
 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:查看答案和解析>>
科目:初中数学 来源:2005年浙江省杭州市中考数学试卷(解析版) 题型:解答题
 (2005•杭州)为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
(2005•杭州)为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com