
 解:(1)如图1,根据图形间的关系,可得△ABC绕A顺时针旋转60°可与△ABF重合,△ABC绕B逆时针旋转60°可与△ABF重合,△ABC绕AB的中点O旋转180°可与△ABF重合;
解:(1)如图1,根据图形间的关系,可得△ABC绕A顺时针旋转60°可与△ABF重合,△ABC绕B逆时针旋转60°可与△ABF重合,△ABC绕AB的中点O旋转180°可与△ABF重合;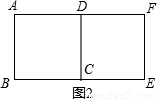


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
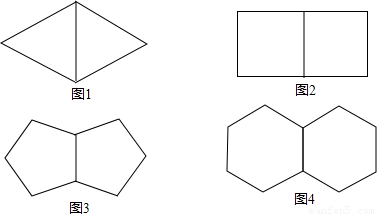
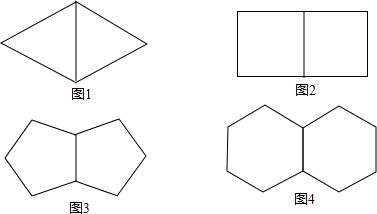
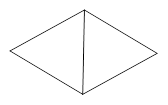
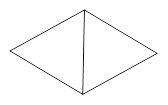
1.如图1是两个有一边重合的正三角形,那么由其中一个正三角形绕平面内某一点旋转后能与另一个正三角形重合,平面内可以作为旋转中心的点有 _ 个.
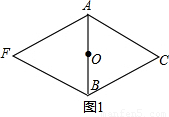
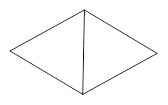
2.如图2是两个有一边重合的正方形,那么由其中一个正方形绕平面内某一点旋转后能与另一个正方形重合,平面内可以作为旋转中心的点有 _ 个.
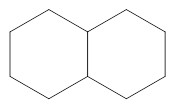
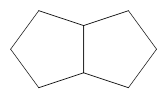
3.如图3是两个有一边重合的正五边形,那么由其中一个正五边形绕平面内某一点旋转后能与另一个正五边形重合,平面内可以作为旋转中心的点有 _ 个.
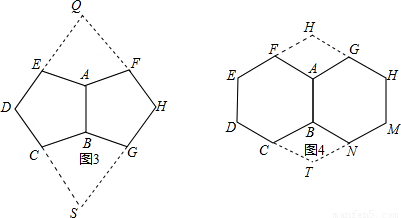
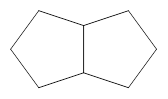
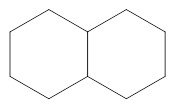
4.如图4是两个有一边重合的正六边形,那么由其中一个正六边形绕平面内某一点旋转后能与另一个正六边形重合,平面内可以作为旋转中心的点有 _ 个.
5.拓展探究:两个有一边重合的正n(n≥3)边形,那么由其中一个正n边形绕平面内某一点旋转后能与另一个正n边形重合,平面内可以作为旋转中心的点有多少个?(直接写结论)
|
|

|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
|
|

|
|
查看答案和解析>>
科目:初中数学 来源:2012届江苏省无锡市惠山区九年级5月模拟考试数学试卷(带解析) 题型:解答题
【小题1】如图1是两个有一边重合的正三角形,那么由其中一个正三角形绕平面内某一点旋转后能与另一个正三角形重合,平面内可以作为旋转中心的点有_ 个.
【小题2】如图2是两个有一边重合的正方形,那么由其中一个正方形绕平面内某一点旋转后能与另一个正方形重合,平面内可以作为旋转中心的点有_ 个.
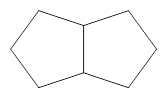
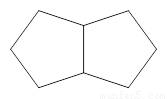
【小题3】如图3是两个有一边重合的正五边形,那么由其中一个正五边形绕平面内某一点旋转后能与另一个正五边形重合,平面内可以作为旋转中心的点有_ 个.
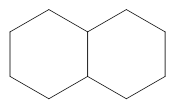
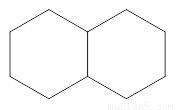
【小题4】如图4是两个有一边重合的正六边形,那么由其中一个正六边形绕平面内某一点旋转后能与另一个正六边形重合,平面内可以作为旋转中心的点有_ 个.
【小题5】拓展探究:两个有一边重合的正n(n≥3)边形,那么由其中一个正n边形绕平面内某一点旋转后能与另一个正n边形重合,平面内可以作为旋转中心的点有多少个?(直接写结论)
|
|

|
|
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省无锡市惠山区九年级5月模拟考试数学试卷(解析版) 题型:解答题
1.如图1是两个有一边重合的正三角形,那么由其中一个正三角形绕平面内某一点旋转后能与另一个正三角形重合,平面内可以作为旋转中心的点有 _ 个.
2.如图2是两个有一边重合的正方形,那么由其中一个正方形绕平面内某一点旋转后能与另一个正方形重合,平面内可以作为旋转中心的点有 _ 个.
3.如图3是两个有一边重合的正五边形,那么由其中一个正五边形绕平面内某一点旋转后能与另一个正五边形重合,平面内可以作为旋转中心的点有 _ 个.
4.如图4是两个有一边重合的正六边形,那么由其中一个正六边形绕平面内某一点旋转后能与另一个正六边形重合,平面内可以作为旋转中心的点有 _ 个.
5.拓展探究:两个有一边重合的正n(n≥3)边形,那么由其中一个正n边形绕平面内某一点旋转后能与另一个正n边形重合,平面内可以作为旋转中心的点有多少个?(直接写结论)
|
|


|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com