
(1)如图1,以 的边
的边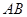 、
、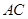 为边分别向外作正方形
为边分别向外作正方形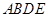 和正方形
和正方形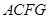 ,连结
,连结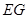 ,试判断
,试判断 与
与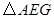 面积之间的关系,并说明理由;
面积之间的关系,并说明理由;
(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形大理石和黑色的三角形大理石铺成.已知中间的所有正方形的面积之和是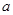 平方米,内圈的所有三角形的面积之和是
平方米,内圈的所有三角形的面积之和是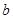 平方米,这条小路一共占地多少平方米?
平方米,这条小路一共占地多少平方米?
(1)相等;(2)(a+2b)平方米.
【解析】
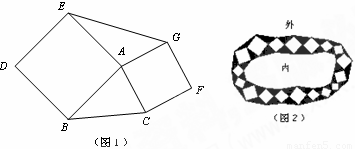
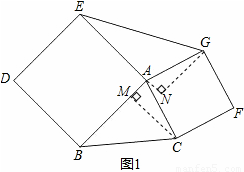
试题分析:(1)过点C作CM⊥AB于M,过点G作GN⊥EA交EA延长线于N,得出△ABC与△AEG的两条高,由正方形的特殊性证明△ACM≌△AGN,是判断△ABC与△AEG面积之间的关系的关键;
(2)同(1)道理知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和,求出这条小路一共占地多少平方米.
试题解析:(1)△ABC与△AEG面积相等.
理由:过点C作CM⊥AB于M,过点G作GN⊥EA交EA延长线于N,则∠AMC=∠ANG=90°,
∵四边形ABDE和四边形ACFG都是正方形,
∴∠BAE=∠CAG=90°,AB=AE,AC=AG,
∵∠BAE+∠CAG+∠BAC+∠EAG=360°,
∴∠BAC+∠EAG=180°,
∵∠EAG+∠GAN=180°,
∴∠BAC=∠GAN,
∴△ACM≌△AGN,
∴CM=GN,
∵S△ABC=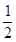 AB•CM,S△AEG=
AB•CM,S△AEG=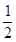 AE•GN,
AE•GN,
∴S△ABC=S△AEG;
(2)由(1)知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和.
∴这条小路的面积为(a+2b)平方米.
考点:1.正方形的性质;2.全等三角形的面积和性质;3.三角形的面积公式.


科目:初中数学 来源: 题型:
归纳和猜想
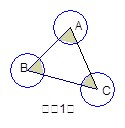
1.如图1,△ABC各边长都大于2,分别以A、B、C为圆心,以1单位长为半径画圆,则阴影部分面积为 .
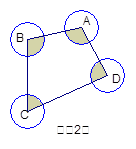
2.如图2,将⑴中的△ABC换成四边形ABCD,其它条件不变,则阴影部分面积为 .
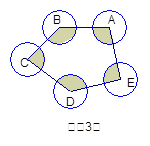
3.如图3,将四边形换成五边形,那么其阴影部分面积为 .
4.根据结论⑴,⑵,⑶,你能总结![]() 边形的情况吗? .
边形的情况吗? .
查看答案和解析>>
科目:初中数学 来源: 题型:
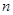 边形的情况吗? .
边形的情况吗? .查看答案和解析>>
科目:初中数学 来源:2011—2012学年北京三十一中初一第二学期期中数学试卷(带解析) 题型:解答题
归纳和猜想
【小题1】如图1,△ABC各边长都大于2,分别以A、B、C为圆心,以1单位长为半径画圆,则阴影部分面积为 .
【小题2】如图2,将⑴中的△ABC换成四边形ABCD,其它条件不变,则阴影部分面积为 .
【小题3】如图3,将四边形换成五边形,那么其阴影部分面积为 .
【小题4】根据结论⑴,⑵,⑶,你能总结 边形的情况吗? .
边形的情况吗? .
查看答案和解析>>
科目:初中数学 来源:2014届北京三十一中初一第二学期期中数学试卷(解析版) 题型:解答题
归纳和猜想
1.如图1,△ABC各边长都大于2,分别以A、B、C为圆心,以1单位长为半径画圆,则阴影部分面积为 .

2.如图2,将⑴中的△ABC换成四边形ABCD,其它条件不变,则阴影部分面积为 .

3.如图3,将四边形换成五边形,那么其阴影部分面积为 .

4.根据结论⑴,⑵,⑶,你能总结 边形的情况吗?
.
边形的情况吗?
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com