解:(1)∵∠BAC=90°,点D是BC中点,BC=4

,
∴AD=

BC=2

;
(2)连DE、ME,如图,

∵DM>DE,
当ED和EM为等腰三角形EDM的两腰,
∴OE⊥DM,
又∵AD=AC,
∴△ADC为等边三角形,
∴∠CAD=60°,
∴∠DAO=30°,
∴∠DON=60°,
在Rt△ADN中,DN=

AD=

,
在Rt△ODN中,ON=

DN=1,
∴当ON等于1时,三点D、E、M组成的三角形是等腰三角形;
当MD=ME,DE为底边,如图3,

作DH⊥AE,
∵AD=2

,∠DAE=30°,
∴DH=

,∠DEA=60°,DE=2,
∴△ODE为等边三角形,
∴OE=DE=2,OH=1,
∵∠M=∠DAE=30°,
而MD=ME,
∴∠MDE=75°,
∴∠ADM=90°-75°=15°,
∴∠DNO=45°,
∴△NDH为等腰直角三角形,
∴NH=DH=

,
∴ON=

-1;
综上所述,当ON等于1或

-1时,三点D、E、M组成的三角形是等腰三角形;
(3)当⊙O变动时DP-DQ的值不变,DP-DQ=2

.理由如下:
连AP、AQ,如图2,
∵∠C=∠CAD=60°,
而DP⊥AB,
∴AC∥DP,
∴∠PDB=∠C=60°,
又∵∠PAQ=∠PDB,
∴∠PAQ=60°,
∴∠CAQ=∠PAD,
∵AC=AD,∠AQC=∠P,
∴△AQC≌△APD,
∴DP=CQ,
∴DP-DQ=CQ-DQ=CD=2

.
分析:(1)根据直角三角形斜边上的中线等于斜边的一半即可得到AD的长;
(2)连DE、ME,易得当ED和EM为等腰三角形EDM的两腰,根据垂径定理得推论得OE⊥DM,易得到△ADC为等边三角形,得∠CAD=60°,则∠DAO=30°,∠DON=60°,然后根据含30°的直角三角形三边的关系得DN=

AD=

,ON=

DN=1;
当MD=ME,DE为底边,作DH⊥AE,由于AD=2

,∠DAE=30°,得到DH=

,∠DEA=60°,DE=2,于是OE=DE=2,OH=1,
又∠M=∠DAE=30°,MD=ME,得到∠MDE=75°,则∠ADM=90°-75°=15°,可得到∠DNO=45°,根据等腰直角三角形的性质得到NH=DH=

,则ON=

-1;
(3)连AP、AQ,DP⊥AB,得AC∥DP,则∠PDB=∠C=60°,再根据圆周角定理得∠PAQ=∠PDB,∠AQC=∠P,则∠PAQ=60°,∠CAQ=∠PAD,易证得△AQC≌△APD,得到
DP=CQ,则DP-DQ=CQ-DQ=CD,而△ADC为等边三角形,CD=AD=2

,即可得到DP-DQ的值.
点评:本题考查了垂径定理和圆周角定理:平分弧的直径垂直弧所对的弦;在同圆和等圆中,相等的弧所对的圆周角相等.也考查了等腰三角形的性质以及含30°的直角三角形三边的关系.

 ,过A,D两点作⊙O,交AB于点E,
,过A,D两点作⊙O,交AB于点E,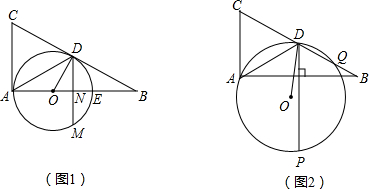
 ,
, BC=2
BC=2 ;
; ∵DM>DE,
∵DM>DE, AD=
AD= ,
, DN=1,
DN=1, 作DH⊥AE,
作DH⊥AE, ,∠DAE=30°,
,∠DAE=30°, ,∠DEA=60°,DE=2,
,∠DEA=60°,DE=2, ,
, -1;
-1; -1时,三点D、E、M组成的三角形是等腰三角形;
-1时,三点D、E、M组成的三角形是等腰三角形; .理由如下:
.理由如下: .
. AD=
AD= ,ON=
,ON= DN=1;
DN=1; ,∠DAE=30°,得到DH=
,∠DAE=30°,得到DH= ,∠DEA=60°,DE=2,于是OE=DE=2,OH=1,
,∠DEA=60°,DE=2,于是OE=DE=2,OH=1, ,则ON=
,则ON= -1;
-1; ,即可得到DP-DQ的值.
,即可得到DP-DQ的值.

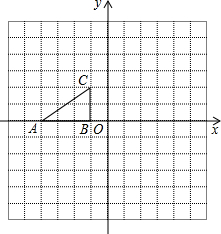 如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.
如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.