
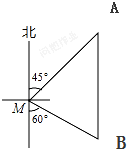
 如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处.求渔船从A到B的航行距离.
如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处.求渔船从A到B的航行距离. 分析 根据题意可以作过点M作MC⊥AB于点C,构造两个直角三角形,然后根据题意可以求得∠AMC和∠BMC的度数,以及边AC、MC、BC的长,从而可以求得AB的长,从而本题得以解决.
解答 解:过点M作MC⊥AB于点C,如下图所示: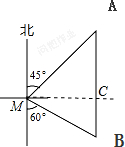
∵由题意可得,∠AMC=90°-45°=45°,∠ACM=∠BCM=90°,∠BMC=90°-60°=30°,AM=180,
又∵sin∠AMC=$\frac{AC}{AM}$,
∴AC=AM•sin45°=$180×\frac{\sqrt{2}}{2}$=90$\sqrt{2}$,
∴MC=AC=90$\sqrt{2}$,
∵tan∠CMB=$\frac{BC}{CM}$
∴BC=tan30°•CM=$\frac{\sqrt{3}}{3}×90\sqrt{2}=30\sqrt{6}$
∴AB=AC+BC=$90\sqrt{2}+30\sqrt{6}$
即渔船从A到B的航行距离是($90\sqrt{2}+30\sqrt{6}$)海里.
点评 本题考查解直角三角形的应用--方向角问题,解题的关键是构造直角三角形,根据直角三角形中锐角三角函数值求出相应的边的长度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com