
分析 (1)根据负整数幂和根式进行计算即可;
(2)根据分式的化简求值解答即可,利用整体代入的思想解决问题.
解答 解:(1)($\frac{1}{3}$)-1-($\sqrt{5}$-2)0+$\sqrt{18}$-(-2)2$•\sqrt{2}$
=$3-1+3\sqrt{2}-4\sqrt{2}$
=2-$\sqrt{2}$;
(2)由x2-x-1=0可得:x2=x+1
化简($\frac{x-1}{x}$-$\frac{x-2}{x+1}$)÷$\frac{2{x}^{2}-x}{{x}^{2}+2x+1}$
=$\frac{(x-1)(x+1)-x(x-2)}{x(x+1)}×\frac{(x+1)^{2}}{x(2x-1)}$
=$\frac{2x-1}{x}×\frac{x+1}{x(2x-1)}$
=$\frac{x+1}{{x}^{2}}$.
∵x2=x+1,
∴上式=$\frac{x+1}{x^2}$=1.
点评 此题考查分式的化简问题,关键是根据分式的化简求值解答.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:解答题
 △AOB在平面直角坐标系中的位置如图所示,其中,A(0,-3),B(-2,0),O是坐标原点.
△AOB在平面直角坐标系中的位置如图所示,其中,A(0,-3),B(-2,0),O是坐标原点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
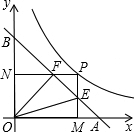 已知:如图所示,动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=-x+1交于点E、F.
已知:如图所示,动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=-x+1交于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
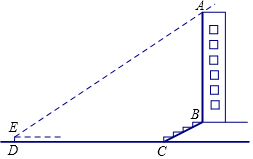 某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com