练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．如图，在梯形ABCD中，AD∥BC，连接AC、BD，则图中面积相等的三角形共有（　　）
    A．4对B．1对C．2对D．3对

    分析 首先过点A作AE⊥BC于点E，过点D作DF⊥BC于点F，由AD∥BC，即可得AE=DF，继而求得S△ABC=S△DBC，S△ABD=S△CAD，则可证得S△AOB=S△DOC．

    解答 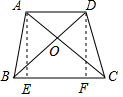解：过点A作AE⊥BC于点E，过点D作DF⊥BC于点F，
    ∵在梯形ABCD中，AD∥BC，
    ∴AE=DF，
    ∵S△ABC=$\frac{1}{2}$BC•AE，S△DBC=$\frac{1}{2}$BC•DF，
    ∴S△ABC=S△DBC，
    同理：S△ABD=S△CAD，
    ∵S△ABC-S△OBC=S△DBC-S△OBC，
    ∴S△AOB=S△DOC；
    ∴图中面积相等的三角形共有3对．
    故选D．

    点评 此题考查了梯形的性质．注意准确作出辅助线是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．△ABC中，AB=AC，∠BAC=120°，AD是BC边上的中线，且BD=BE，求∠AED的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．红星中学为了解七年级学生课堂发言情况，随机抽取该年级部分学生，对他们某天在课堂上发言的次数进行了统计，其结果如表，并绘制了如图所示的两幅不完整的统计图，已知B、E两组发言人数的比为5：2，请结合图中相关数据回答下列问题：
    （1）求出样本容量，并补全直方图；
    （2）该年级共有学生600人，请估计全年级在这天里发言次数不少于12次的人数；
    （3）已知A组发言的学生中恰有2位女生，E组发言的学生中恰有1位男生，现从A组与E组中分别抽一位学生写报告，请用列表法或画树状图的方法，求所抽的两位学生恰好是一男一女的概率．
    发言次数n
    A0≤n＜3
    B3≤n＜6
    C6≤n＜9
    D9≤n＜12
    E12≤n＜15
    F15≤n＜18

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．（1）在图中的平面图形可以围成哪种几何体？
    （2）小圆的周长和大半圆的弧长有什么关系？
    （3）小圆的半径r和大半圆的半径R之间有什么关系？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．已知|a|=2，|b|=3，则|a-b|=5的概率为（　　）
    A．0B．$\frac{1}{2}$C．$\frac{1}{3}$D．$\frac{1}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．在△ABC中，AB=m，AC=n，P是AB的中点，过P点的直线交AC边于Q点，若以A、P、Q为顶点的三角形和以A、B、C为顶点的三角形相似，则AQ的长为（　　）
    A．$\frac{m}{2}$B．$\frac{n}{2}$C．$\frac{m}{2}$或$\frac{{n}^{2}}{2m}$D．$\frac{n}{2}$或$\frac{{m}^{2}}{2n}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，已知正方形A1B1C1D1的面积为1，把它的各边延长一倍得到新的正方形A2B2C2D2，再将正方形A2B2C2D2各边长延长一倍得到正方形A3B3C3D3，以此下去…，则正方形A9B9C9D9的周长是2500．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知ab≠0，且M=$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$，当a，b，c取不同值时，M有4种不同可能．
    当a，b，c都是正数时，M=3．
    当a，b，c中有一个负数时，M=1．
    当a，b，c中有二个负数时，M=-1．
    当a，b，c都是负数时，M=-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．将下列推理过程中的依据补充完整．
    已知：如图：∠1=∠2，且BE平分∠ABC，求证：∠AED=∠C．
    证明：∵BE平分∠ABC（已知），
    ∴∠1=∠EBC（角平分线的定义）
    又∵∠1=∠2（已知）
    ∴∠2=∠EBC（等量代换）
    ∴DE∥BC（内错角相等，两直线平行）
    ∴∠AED=∠C（两直线平行，同位角相等）

    查看答案和解析>>

    同步练习册答案